Question

已知椭圆的右焦点为F，右准线为l，A、B是椭圆上两点，且|AF|：|BF|=3：2，直线AB与l交于点C，则B分有向线段

AC

所成的比为（　　）

• A、

  1

  2

• B、2
• C、

  2

  3

• D、

  3

  2

Answer 1

分析：先分别过A，B作准线的垂线AM，BN，如图，由椭圆第二定义知：|AF|=e|AM|，|BF|=e|BN|，于是得出|AM|：|BN|，在三角形AMC中，因AM平行于BN，根据三角形相似得到|AC|：|BC|=|AM|：|BN|=3：2最后即可得出B分有向线段

AC

所成的比．

解答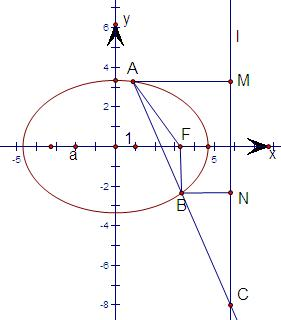：解：分别过A，B作准线的垂线AM，BN，如图，
由椭圆第二定义知：|AF|=e|AM|，|BF|=e|BN|，
于是有：|AM|：|BN|=|AF|：|BF|=3：2，
在三角形AMC中，因AM平行于BN，
故|AC|：|BC|=|AM|：|BN|=3：2，
则B分有向线段

AC

所成的比为|AB|：|BC|=1：2．
故选A．

点评：本题考查椭圆的简单性质、第二定义，椭圆的标准方程，以及三角形的相似的性质．