题目内容
已知椭圆 的右焦点为
的右焦点为 ,上顶点为B,离心率为
,上顶点为B,离心率为 ,圆
,圆 与
与 轴交于
轴交于 两点
两点
(Ⅰ)求 的值;
的值;
(Ⅱ)若 ,过点
,过点 与圆
与圆 相切的直线
相切的直线 与
与 的另一交点为
的另一交点为 ,求
,求 的面积
的面积
【答案】
①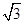 ②
②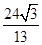
【解析】
试题分析:(Ⅰ)利用圆及椭圆方程求出点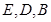 的坐标, 再用离心率值化简,利用两点间距离即可 (Ⅱ)由椭圆方程,利用圆的切线性质确定直线
的坐标, 再用离心率值化简,利用两点间距离即可 (Ⅱ)由椭圆方程,利用圆的切线性质确定直线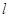 的斜率,写出直线方程,再与椭圆方程联立,求出交点坐标后求弦
的斜率,写出直线方程,再与椭圆方程联立,求出交点坐标后求弦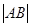 的长
,及点到直线距离即可
的长
,及点到直线距离即可
试题解析:
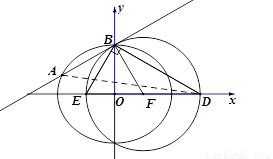
(Ⅰ)由题意,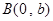 ,
,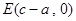 ,
,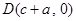 ,∵
,∵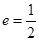
得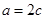 ,
,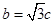
则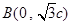 ,
,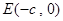 ,
,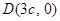
得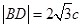 ,
,
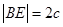
则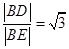 ………(4分)
………(4分)
(Ⅱ)当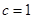 时,
时,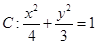 ,
,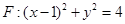
得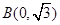 在圆F上
在圆F上
直线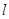
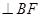 ,则设
,则设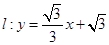
由 得
得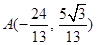 ,
,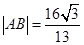
又点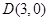 到直线
到直线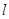 的距离
的距离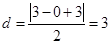 ,
,
得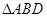 的面积
的面积
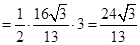 (12分)
(12分)
考点:1 椭圆的定义;2 离心率;3 圆的几何性质;4 直线与椭圆位置关系的运算;5 点到直线的距离公式

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目




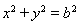

 的右焦点为
的右焦点为 ,
, 点在椭圆上,以
点在椭圆上,以 轴相切,且同时与
轴相切,且同时与 轴相切于椭圆的右焦点
轴相切于椭圆的右焦点 的离心率为 .
的离心率为 . 的右焦点为
的右焦点为 且
且 ,设短轴的一个端点为
,设短轴的一个端点为 ,原点
,原点 到直线
到直线 的距离为
的距离为 ,过原点和
,过原点和 轴不重合的直线与椭圆
轴不重合的直线与椭圆 相交于
相交于 两点,且
两点,且 .
. 的直线
的直线 与椭圆
与椭圆 且使得
且使得 成立?若存在,试求出直线
成立?若存在,试求出直线