题目内容
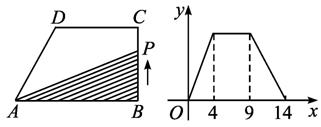
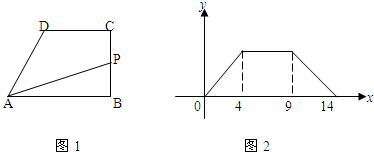
直角梯形ABCD如图1,动点P从点B出发,由B→C→D→A沿边运动,设点P运动的路程为x,△ABP的面积为f(x).如果函数y=f(x)的图象如图2所示,则△ABC的面积为( )

| A、10 | B、32 | C、18 | D、16 |
分析:由y=f(x)的图象可知,当x由0→4时,f(x)由0变成最大,说明BC=4,由x从4→9时f(x)不变,说明此时P点在DC上,即CD=5,由x从9→14时f(x)变为0,说明此时P点在AD上,即AD=5.所以可求AB的长,最后求出答案.
解答: 解:由题意知,BC=4,CD=5,AD=5
解:由题意知,BC=4,CD=5,AD=5
过D作DG⊥AB
∴AG=3,由此可求出AB=3+5=8.
S△ABC=
AB•BC=
×8×4=16.
故选D.
 解:由题意知,BC=4,CD=5,AD=5
解:由题意知,BC=4,CD=5,AD=5过D作DG⊥AB
∴AG=3,由此可求出AB=3+5=8.
S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
故选D.
点评:要能根据函数图象的性质和图象上的数据分析得出函数的类型和所需要的条件,结合实际意义得到正确的结论.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
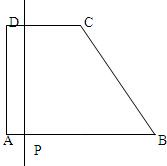
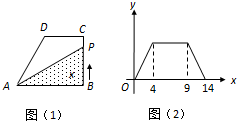 直角梯形ABCD如图(1),动点P从B点出发,由B→C→D→A沿边运动,设点P运动的距离为x,△ABP的面积为f (x),如果函数y=f (x)的图象如图(2),则梯形ABCD的面积为( )
直角梯形ABCD如图(1),动点P从B点出发,由B→C→D→A沿边运动,设点P运动的距离为x,△ABP的面积为f (x),如果函数y=f (x)的图象如图(2),则梯形ABCD的面积为( )