题目内容
【题目】在平面直角坐标系中,以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,过点
,过点![]() 的直线
的直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),直线
为参数),直线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
,![]() 两点.
两点.
(1)写出曲线![]() 的直角坐标方程和直线
的直角坐标方程和直线![]() 的普通方程;
的普通方程;
(2)若![]() ,求
,求![]() 的值.
的值.
【答案】(1)曲线![]() 的直角坐标方程
的直角坐标方程![]() ,直线
,直线![]() 的普通方程为
的普通方程为![]() ;(2)
;(2)![]() 。
。
【解析】
(1)利用代入法消去直线![]() 的参数方程中的参数,可得其普通方程,曲线
的参数方程中的参数,可得其普通方程,曲线![]() 的极坐标方程两边同乘以
的极坐标方程两边同乘以![]() ,利用
,利用![]() 即可得到曲线
即可得到曲线![]() 的直角坐标方程;(2)直线
的直角坐标方程;(2)直线![]() 的参数方程代入曲线
的参数方程代入曲线![]() 的直角坐标方程,利用韦达定理、直线参数方程的几何意义可得结果.
的直角坐标方程,利用韦达定理、直线参数方程的几何意义可得结果.![]()
(1)由![]() 得
得![]() ,
,
所以曲线![]() 的直角坐标方程
的直角坐标方程![]() ,
,
因为![]() ,所以
,所以![]() ,
,
直线![]() 的普通方程为
的普通方程为![]() ;
;
(2)直线![]() 的参数方程为
的参数方程为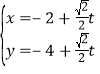 (
(![]() 为参数),
为参数),
代入![]() 得:
得:![]() ,
,
设![]() ,
,![]() 对应的参数分别为
对应的参数分别为![]() ,
,![]() ,
,
则![]() ,
,![]() ,
,![]() ,
,![]()
由参数![]() ,
,![]() 的几何意义得
的几何意义得![]() ,
,![]() ,
,![]() ,
,
由![]() 得
得![]() ,所以
,所以![]() ,
,
所以![]() ,即
,即![]() ,
,
故![]() ,或
,或![]() (舍去),
(舍去),
所以![]() .
.

【题目】为推进“千村百镇计划”,2019年4月某新能源公司开展“电动绿色出行”活动,首批投放200台![]() 型新能源车到某地多个村镇,供当地村民免费试用三个月.试用到期后,为了解男女试用者对
型新能源车到某地多个村镇,供当地村民免费试用三个月.试用到期后,为了解男女试用者对![]() 型新能源车性能的评价情况,该公司要求每位试用者填写一份性能综合评分表(满分为100分).最后该公司共收回有效评分表600份,现从中随机抽取40份(其中男、女的评分表各20份)作为样本,经统计得到茎叶图:
型新能源车性能的评价情况,该公司要求每位试用者填写一份性能综合评分表(满分为100分).最后该公司共收回有效评分表600份,现从中随机抽取40份(其中男、女的评分表各20份)作为样本,经统计得到茎叶图:
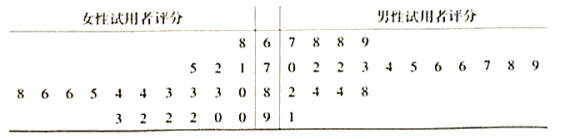
(1)求40个样本数据的中位数![]() ;
;
(2)已知40个样本数据的平均数![]() ,记
,记![]() 与
与![]() 的最大值为
的最大值为![]() .该公司规定样本中试用者的“认定类型”:评分不小于
.该公司规定样本中试用者的“认定类型”:评分不小于![]() 的为“满意型”,评分小于
的为“满意型”,评分小于![]() 的为“需改进型”.
的为“需改进型”.
①请以40个样本数据的频率分布来估计收回的600份评分表中,评分小于![]() 的份数;
的份数;
②请根据40个样本数据,完成下面2×2列联表:
认定类型 性别 | 满意型 | 需改进型 | 合计 |
女性 | 20 | ||
男性 | 20 | ||
合计 | 40 |
根据2×2列联表判断能否有99%的把握认为“认定类型”与性别有关?
附: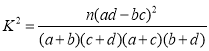 .
.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |