题目内容
已知α,β是三次函数f(x)=
x3+
ax2+2bx的两个极值点,且α∈(0,1),β∈(1,2),则
的取值范围是( )
| 1 |
| 3 |
| 1 |
| 2 |
| b-2 |
| a-1 |
A、(
| ||||
B、(
| ||||
C、(-
| ||||
D、(-
|
分析:由已知中α,β是三次函数f(x)=
x3+
ax2+2bx的两个极值点,且α∈(0,1),β∈(1,2),我们易得f′(x)=x2+ax+2b的两个零点分别在区间(0,1)和(1,2)上,由零点存在定理,我们易构造关于a,b的不等式组,将问题转化为一个线性规划问题,分析
的几何意义,即可根据数形结合求出答案.
| 1 |
| 3 |
| 1 |
| 2 |
| b-2 |
| a-1 |
解答: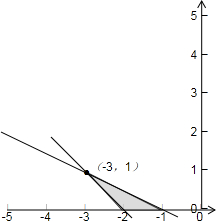 解:∵函数f(x)=
解:∵函数f(x)=
x3+
ax2+2bx
∴f′(x)=x2+ax+2b
又∵α∈(0,1),β∈(1,2),
∴
其对应的平面区域如下图所示:
由图可得:当x=-3,y=1时,
取最小值
;
当x=-1,y=0时,
取最大值1;
故选A
 解:∵函数f(x)=
解:∵函数f(x)=| 1 |
| 3 |
| 1 |
| 2 |
∴f′(x)=x2+ax+2b
又∵α∈(0,1),β∈(1,2),
∴
|
其对应的平面区域如下图所示:
由图可得:当x=-3,y=1时,
| b-2 |
| a-1 |
| 1 |
| 4 |
当x=-1,y=0时,
| b-2 |
| a-1 |
故选A
点评:本题考查的知识点是函数在某点取得极值的条件,其中根据函数在某点取得极值的条件,将问题转化为函数的零点问题,再根据零点存在定理,将问题转化为线性规划问题是解答本题的关键.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
 的两个极值点,且x1∈(0,1),x2∈(1,2),则a-2b的范围是
的两个极值点,且x1∈(0,1),x2∈(1,2),则a-2b的范围是 的两个极值点,且x1∈(0,1),x2∈(1,2),则a-2b的范围是( )
的两个极值点,且x1∈(0,1),x2∈(1,2),则a-2b的范围是( )