题目内容
已知x1,x2为三次函数f(x)= 的两个极值点,且x1∈(0,1),x2∈(1,2),则a-2b的范围是
的两个极值点,且x1∈(0,1),x2∈(1,2),则a-2b的范围是
- A.(-5,-2)
- B.(-2,-1)
- C.(-5,-1)
- D.(-∞,-1)
C
分析:根据极值的意义可知,极值点x1、x2是导函数等于零的两个根,根据根的分布建立不等关系,画出满足条件的区域,明确目标函数的几何意义,即可求得结论.
解答: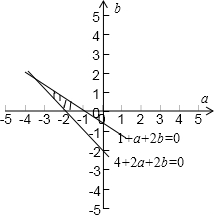 解:求导函数可得f'(x)=x2+ax+2b
解:求导函数可得f'(x)=x2+ax+2b
依题意知,方程f'(x)=0有两个根x1、x2,且x1∈(0,1),x2∈(1,2),
等价于f'(0)>0,f'(1)<0,f'(2)>0.
∴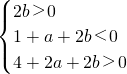 .
.
满足条件的(a,b)的平面区域为图中阴影部分,
三角形的三个顶点坐标为(-1,0),(-2,0),(-3,1),
分别代入a-2b得:-1-2×0=-1,-2-2×0=-2,-3-2×1=-5.
∴a-2b的范围是(-5,-1),
故选C.
点评:本题主要考查了利用导数研究函数的极值,以及二元一次不等式(组)与平面区域,属于中档题.
分析:根据极值的意义可知,极值点x1、x2是导函数等于零的两个根,根据根的分布建立不等关系,画出满足条件的区域,明确目标函数的几何意义,即可求得结论.
解答:
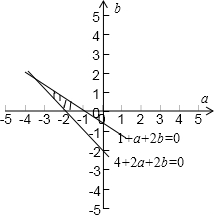 解:求导函数可得f'(x)=x2+ax+2b
解:求导函数可得f'(x)=x2+ax+2b依题意知,方程f'(x)=0有两个根x1、x2,且x1∈(0,1),x2∈(1,2),
等价于f'(0)>0,f'(1)<0,f'(2)>0.
∴
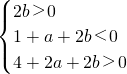 .
.满足条件的(a,b)的平面区域为图中阴影部分,
三角形的三个顶点坐标为(-1,0),(-2,0),(-3,1),
分别代入a-2b得:-1-2×0=-1,-2-2×0=-2,-3-2×1=-5.
∴a-2b的范围是(-5,-1),
故选C.
点评:本题主要考查了利用导数研究函数的极值,以及二元一次不等式(组)与平面区域,属于中档题.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
 的两个极值点,且x1∈(0,1),x2∈(1,2),则a-2b的范围是( )
的两个极值点,且x1∈(0,1),x2∈(1,2),则a-2b的范围是( )