Question

已知实数x，y满足|x|+|y|≤1，则2x+y的最大值为（　　）

• A、

  1

  3

• B、

  1

  2

• C、1
• D、2

Answer 1

分析：先根据约束条件画出可行域，设z=2x+y，再利用z的几何意义求最值，只需求出直线z=2x+y过可行域内的角点时，从而得到z=2x+y的最大值最小值即可．

解答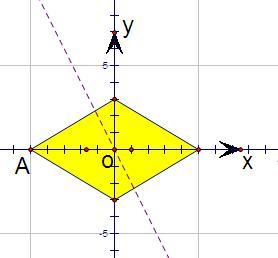：解：先根据约束条件画出可行域，
设z=2x+y，
将z的值转化为直线z=2x+y在y轴上的截距，
当直线z=2x+y经过点（1，0）时，z最大，
最大值为：2．
故选D．

点评：本题主要考查了用平面区域二元一次不等式组，以及简单的转化思想和数形结合的思想，属中档题．目标函数有唯一最优解是我们最常见的问题，这类问题一般要分三步：画出可行域、求出关键点、定出最优解．