题目内容
设定义在R+上的函数y=f(x),对于任意正数x、y都有f(xy)=f(x)+f(y),且当x>1时,f(x)<0,f(3)=-1.
(1)求f(1)和f![]() 的值;
的值;
(2)若不等式f(x)+f(2-x)<2成立,求x的取值范围;(提示:x2-2x+![]() <0
<0![]() 1-
1-![]() <x<1+
<x<1+![]() )
)
(3)若存在正数k,使不等式f(kx)+f(2-x)<2有解,求正数k的取值范围.
答案:
解析:
解析:
|
(1)f(1)=0,f (2)x的取值范围是 (3)不等式f(kx)+f(2-x)<2(k>0)可转化为kx(2-x)> |

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
设定义在R上的函数f(x)同时满足以下条件:①f(x+1)=-f(x)对任意的x都成立;②当x∈[0,1]时,f(x)=ex-e•cos
+m(其中e=2.71828…是自然对数的底数,m是常数).记f(x)在区间[2013,2016]上的零点个数为n,则( )
| πx |
| 2 |
A、m=-
| ||
| B、m=1-e,n=5 | ||
C、m=-
| ||
| D、m=e-1,n=4 |
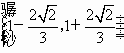 .
.