题目内容

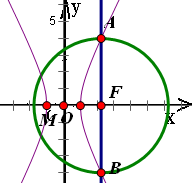
过双曲线的右焦点F作实轴所在直线的垂线，交双曲线于A，B两点，设双曲线的左顶点M，若点M在以AB为直径的圆的内部，则此双曲线的离心率e的取值范围为（　　）
A．(
3
2
，+∞)		B．(1，
3
2
)		C．（2，+∞）D．（1，2）
设双曲线方程为
x2
a2
-
y2
b2
=1，a＞b＞0
则直线AB方程为：x=c，其中c=
a2+b2

因此，设A（c，y0），B（c，-y0），
∴
c2
a2
-
y02
b2
=1，解之得y0=
b2
a
，得|AF|=
b2
a
，
∵双曲线的左焦点M（-a，0）在以AB为直径的圆内部
∴|MF|＜|AF|，即a+c＜
b2
a
，
将b2=c2-a2，并化简整理，得2a2+ac-c2＜0
两边都除以a2，整理得e2-e-2＞0，解之得e＞2（舍负）
故选：C
练习册系列答案
相关题目
与椭圆
x2
6
+y2=1共焦点，且渐近线为y=±2x的双曲线方程是（　　）
A．x2-
y2
4
=1		B．y2-
x2
4
=1		C．
x2
4
-y2=1		D．
y2
4
-x2=1
如图，在△ABC中，∠ABC=∠ACB=30°，AB，AC边上的高分别为CD，BE，则以B，C为焦点且经过D、E两点的椭圆与双曲线的离心率的和为______．
双曲线
x2
a2
-
y2
b2
=1的两焦点分别为F1和F2，若双曲线上存在不是顶点的点P，使得∠PF2F1=3∠PF1F2，则双曲线离心率e的取值范围是______．
双曲线
y2
2
-x2=1的焦点坐标是（　　）
A．（0，±1）B．（±1，0）C．（0，±
3
）		D．（±
3
，0）
双曲线
x2
a2
-
y2
b2
=1（a＞1，b＞0）的焦点距为2c，直线l过点（a，0）和（0，b），且点（1，0）到直线l的距离与点（-1，0）到直线l的距离之和s≥
4
5
c．求双曲线的离心率e的取值范围．
求以椭圆3x2+13y2=39的焦点为焦点，以直线y=±
x
2
为渐近线的双曲线方程．
已知双曲线
x2
a2
-
y2
b2
=1(a＞b＞0)的两条渐近线的夹角为
π
3
，则双曲线的离心率为______．
已知双曲线
x2
16
-
y2
9
=1的左、右焦点分别为F1，F2，若双曲线上一点P使∠F1PF2=90°，则△F1PF2的面积是______．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网