题目内容

如图，在△ABC中，∠ABC=∠ACB=30°，AB，AC边上的高分别为CD，BE，则以B，C为焦点且经过D、E两点的椭圆与双曲线的离心率的和为______．
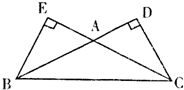
设|BC|=2c，则|BF|=|CD|=c，|CF|=|BD|=
3
c．
由题意可得c+
3
c=2a，
3
c-c=2a′（2a为椭圆的长轴长，2a′为双曲线的实轴长）．
∴
c
a
=
2
1+
3
=
3
-1，
c
a′
=
2
3
-1
=
3
+1．
∴
c
a
+
c
a′
=2
3
．
故答案为2
3
．
练习册系列答案
相关题目
已知双曲线
x2
a2
-
y2
b2
=1的一条渐近线方程为y=3x，则其离心率为______．
过点（0，4）可作______条直线与双曲线y2-4x2=16有且只有一个公共点．
焦点为F（0，10），渐近线方程为4x±3y=0的双曲线的方程是（　　）
A．
y2
64
-
x2
36
=1		B．
x2
9
-
y2
16
=1
C．
y2
9
-
x2
16
=1		D．
x2
64
-
y2
36
=1
焦点为（3，0），且与双曲线
x2
2
-y2=1有相同的渐近线的双曲线方程是______．
点P是双曲线
x2
4
-y2=1的右支上一点，M、N分别是圆(x+
5
)2+y2=1和圆(x-
5
)2+y2=1上的点，则|PM|-|PN|的最大值是______．
在相距4k米的A、B两地，听到炮弹爆炸声的时间相差2秒，若声速每秒k米，则爆炸地点P必在（　　）
A．以A，B为焦点，短轴长为
3
k米的椭圆上．
B．以A，B为焦点，实轴长为2k米的双曲线上．
C．以AB为直径的圆上．
D．以A，B为顶点，虚轴长为
3
k米的双曲线上．
过双曲线的右焦点F作实轴所在直线的垂线，交双曲线于A，B两点，设双曲线的左顶点M，若点M在以AB为直径的圆的内部，则此双曲线的离心率e的取值范围为（　　）
A．(
3
2
，+∞)		B．(1，
3
2
)		C．（2，+∞）D．（1，2）
过点P（2，1）的双曲线与椭圆
x2
4
+y2=1共焦点，则其渐近线方程是______．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网