题目内容
数列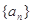 的前n项和记为
的前n项和记为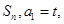 点
点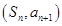 在直线
在直线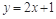 上,
上,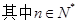 .(1)若数列
.(1)若数列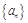 是等比数列,求实数
是等比数列,求实数 的值;
的值;
(2)设各项均不为0的数列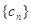 中,所有满足
中,所有满足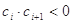 的整数
的整数 的个数称为这个数列
的个数称为这个数列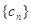 的“积异号数”,令
的“积异号数”,令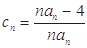 (
(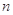
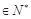 ),在(1)的条件下,求数列
),在(1)的条件下,求数列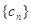 的“积异号数”
的“积异号数”
(1)1 (2)1
解析试题分析:(1)根据数列的第n项与前n项和的关系可得n≥2时,有 ,化简得an+1=3an(n≥2),要使n≥1时{an}是等比数列,只需
,化简得an+1=3an(n≥2),要使n≥1时{an}是等比数列,只需 ,从而得出t的值.
,从而得出t的值.
(2)由条件求得cn=1? =
=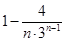 ,计算可得c1c2=-1<0,再由cn+1-cn>0可得,数列{cn}递增,由c2=
,计算可得c1c2=-1<0,再由cn+1-cn>0可得,数列{cn}递增,由c2= >0,得当n≥2时,cn>0,由此求得数列{cn}的“积异号数”为1.
>0,得当n≥2时,cn>0,由此求得数列{cn}的“积异号数”为1.
(1)由题意,当 时,有
时,有
两式相减,得 , 3分
, 3分
所以,当 时
时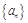 是等比数列,要使
是等比数列,要使 时
时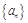 是等比数列,则只需
是等比数列,则只需
从而得出 5分
5分
(2)由(1)得,等比数列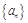 的首项为
的首项为 ,公比
,公比 ,∴
,∴
∴
 7分
7分
∵ ,
, ,∴
,∴
∵ ,
,
∴数列 递增. 10分
递增. 10分
由 ,得当
,得当 时,
时, .
.
∴数列 的“积异号数”为1. 12分
的“积异号数”为1. 12分
考点:1.数列与函数的综合;2.等比关系的确定;3.数列的求和.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
在等差数列{an}中,a2=1,a4=5,则{an}的前5项和S5=( )
| A.7 | B.15 | C.20 | D.25 |
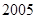 是数列
是数列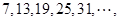 中的第( )项.
中的第( )项.
A.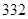 | B. | C. | D. |
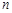 件首饰所用珠宝数为*****颗.
件首饰所用珠宝数为*****颗. 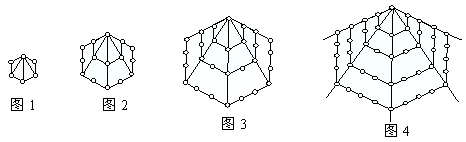
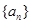 的前
的前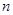 项和为
项和为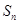 ,且
,且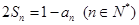 .
.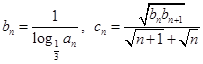 ,求数列
,求数列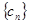 的前
的前 .
.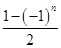 an-
an-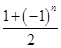 bn,求数列{cn}的前2n项和T2n.
bn,求数列{cn}的前2n项和T2n.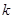 (
(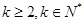 )的数列
)的数列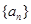 、
、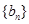 、
、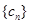 前
前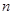 项的和分别为
项的和分别为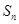 、
、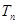 、
、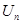 .已知
.已知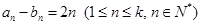 ,且集合
,且集合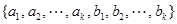 =
=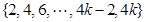 .
. 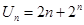 ,求数列
,求数列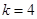 ,求
,求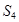 和
和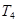 的值,并写出两对符合题意的数列
的值,并写出两对符合题意的数列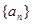 的各项都是1或2.首项为1,且在第
的各项都是1或2.首项为1,且在第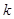 个1和第
个1和第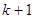 个1之间有
个1之间有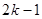 个2,即1,2,1,2,2,2,1,2,2,2,2,2,1,….记数列的前
个2,即1,2,1,2,2,2,1,2,2,2,2,2,1,….记数列的前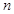 项的和为
项的和为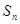 .参考:31×32=992,32×33=1056,44×45=1980,45×46=2070
.参考:31×32=992,32×33=1056,44×45=1980,45×46=2070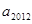 和
和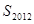 ;
; ,使得
,使得 ?如果存在,求出
?如果存在,求出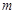 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.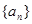 的前
的前 项和
项和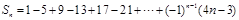 ,则
,则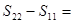 .
.