题目内容
如图, 在直三棱柱ABC-A1B1C1中,AC=4,CB=2,AA1=
在直三棱柱ABC-A1B1C1中,AC=4,CB=2,AA1=
,∠ACB=60°,E、F分别是A1C1、BC的中点.
(1)证明:C1F∥平面ABE;
(2)若P是线段BE上的点,证明:平面A1B1C⊥平面C1FP;
(3)若P在E点位置,求三棱锥P-B1C1F的体积.
 在直三棱柱ABC-A1B1C1中,AC=4,CB=2,AA1=
在直三棱柱ABC-A1B1C1中,AC=4,CB=2,AA1=| 2 |
(1)证明:C1F∥平面ABE;
(2)若P是线段BE上的点,证明:平面A1B1C⊥平面C1FP;
(3)若P在E点位置,求三棱锥P-B1C1F的体积.
分析:(1)取AB中点G,连接GF、GE,可以证出四边形EGFC1为平行四边形,从而得到C1F∥EG,最后结合线面平行判定定理,可得C1F∥平面ABE.
(2)根据线面垂直的判定与性质和题中的直三棱柱性质,证出A1B1⊥C1F且B1C⊥C1F,从而得到C1F⊥平面A1B1C,结合C1F?平面C1FP,可得平面A1B1C⊥平面C1FP.
(3)根据E是A1C1的中点,得到E到平面BCC1B1的距离是A1到平面BCC1B1的距离一半,得到以△B1C1F为底的高等于
A1B1=
,算出△B1C1F的面积并结合锥体体积公式,可算出三棱锥P-B1C1F的体积.
(2)根据线面垂直的判定与性质和题中的直三棱柱性质,证出A1B1⊥C1F且B1C⊥C1F,从而得到C1F⊥平面A1B1C,结合C1F?平面C1FP,可得平面A1B1C⊥平面C1FP.
(3)根据E是A1C1的中点,得到E到平面BCC1B1的距离是A1到平面BCC1B1的距离一半,得到以△B1C1F为底的高等于
| 1 |
| 2 |
| 3 |
解答:解:(1)取AB中点G,连接GF、GE,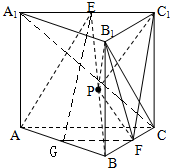
∵F为BC中点,∴FG∥AC,且FG=
AC
而由三棱柱可得,C1E∥AC,且C1E=
AC,∴FG∥C1E且FG=C1E
∴四边形EGFC1为平行四边形,得C1F∥EG,
∵EG?平面ABE,C1F?平面ABE,
∴C1F∥平面ABE.…(5分)
(2)△ABC中,AC=4,CB=2,∠ACB=60°,
可求得AB=2
且∠ABC=90°即AB⊥BC
∵三棱柱ABC-A1B1C1中,△ABC≌△A1B1C1,∴∠A1B1C1也为90°,即A1B1⊥B1C1,
又由直三棱柱可得BB1⊥底面A1B1C1,∴BB1⊥A1B1,
∵BB1∩B1C1=B1,BB1、B1C1?侧面B1C1CB,∴A1B1⊥侧面B1C1CB结合C1F?侧面B1C1CB,得A1B1⊥C1F;
在侧面矩形B1C1CB中,BB1=
,BC=2,F为BC中点
∴△C1CF∽△CBB1,从而得∠BCB1=∠FC1C
∴∠C1FC+∠BCB1=∠C1FC+∠FC1C=90°,即B1C⊥C1F;
又∵A1B1∩B1C=B1,A1B1?平面A1B1C,B1C?平面A1B1C,
∴C1F⊥平面A1B1C
又∵C1F?平面C1FP,
∴平面A1B1C⊥平面C1FP.…(12分)
(3)∵P在E点位置,三棱锥P-B1C1F即为三棱锥E-B1C1F
∵E是A1C1的中点,∴E到平面BCC1B1的距离是A1到平面BCC1B1的距离一半
又∵A1B1⊥平面BCC1B1,且A1B1=2
,∴P到平面BCC1B1的距离d=
A1B1=
而在矩形BCC1B1中,S△B1C1F=
S矩形BCC1B1=
∴V三棱锥=
×S△B1C1F×d=
…(16分)

∵F为BC中点,∴FG∥AC,且FG=
| 1 |
| 2 |
而由三棱柱可得,C1E∥AC,且C1E=
| 1 |
| 2 |
∴四边形EGFC1为平行四边形,得C1F∥EG,
∵EG?平面ABE,C1F?平面ABE,
∴C1F∥平面ABE.…(5分)
(2)△ABC中,AC=4,CB=2,∠ACB=60°,
可求得AB=2
| 3 |
∵三棱柱ABC-A1B1C1中,△ABC≌△A1B1C1,∴∠A1B1C1也为90°,即A1B1⊥B1C1,
又由直三棱柱可得BB1⊥底面A1B1C1,∴BB1⊥A1B1,
∵BB1∩B1C1=B1,BB1、B1C1?侧面B1C1CB,∴A1B1⊥侧面B1C1CB结合C1F?侧面B1C1CB,得A1B1⊥C1F;
在侧面矩形B1C1CB中,BB1=
| 2 |
∴△C1CF∽△CBB1,从而得∠BCB1=∠FC1C
∴∠C1FC+∠BCB1=∠C1FC+∠FC1C=90°,即B1C⊥C1F;
又∵A1B1∩B1C=B1,A1B1?平面A1B1C,B1C?平面A1B1C,
∴C1F⊥平面A1B1C
又∵C1F?平面C1FP,
∴平面A1B1C⊥平面C1FP.…(12分)
(3)∵P在E点位置,三棱锥P-B1C1F即为三棱锥E-B1C1F
∵E是A1C1的中点,∴E到平面BCC1B1的距离是A1到平面BCC1B1的距离一半
又∵A1B1⊥平面BCC1B1,且A1B1=2
| 3 |
| 1 |
| 2 |
| 3 |
而在矩形BCC1B1中,S△B1C1F=
| 1 |
| 2 |
| 2 |
∴V三棱锥=
| 1 |
| 3 |
| ||
| 3 |
点评:本题以特殊的直三棱柱为载体,求证线面平行、面面垂直,并求锥体的体积.着重考查了直线与平面平行的判定、平面与平面垂直的判定和棱锥的体积等知识,属于中档题.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目




