题目内容
设O（0，0），A（1，0），B（0，1），点p是线段AB上的一个动点，
，若
，则实数λ的取值范围是（ ）A．
B．
C．
D．
【答案】分析：根据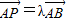
所以可以表示出
，
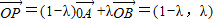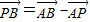=（1-λ）
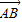=（λ-1，1-λ）
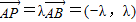，再根据
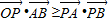，代入即可确定范围．
解答：解：∵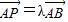
∴
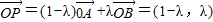
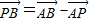=（1-λ）
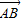=（λ-1，1-λ），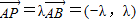
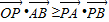
∴（1-λ，λ）•（-1，1）≥（λ，-λ）•（λ-1，1-λ）
∴2λ2-4λ+1≤0
解得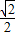：1-
≤λ≤1+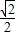
，
因点P是线段AB上的一个动点．
所以0≤λ≤1，即满足条件的实数λ的取值范围是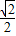1-
≤λ≤1，
故选B．
点评：本题考查向量的表示方法，向量的基本运算，定比分点中定比的范围等等
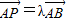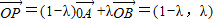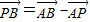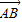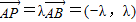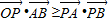所以可以表示出，=（1-λ）=（λ-1，1-λ），再根据，代入即可确定范围．解答：解：∵
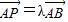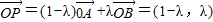
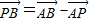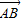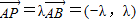
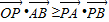
∴=（1-λ）=（λ-1，1-λ），∴（1-λ，λ）•（-1，1）≥（λ，-λ）•（λ-1，1-λ）
∴2λ2-4λ+1≤0
解得：1-
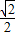≤λ≤1+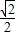，因点P是线段AB上的一个动点．
所以0≤λ≤1，即满足条件的实数λ的取值范围是1-
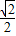≤λ≤1，故选B．
点评：本题考查向量的表示方法，向量的基本运算，定比分点中定比的范围等等
练习册系列答案
双基同步导航训练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
设O（0，0），A（1，0），B（0，1），点p是线段AB上的一个动点，
=λ
，若
•
≥
•
，则实数λ的取值范围是（ ）
| AP |
| AB |
| OP |
| AB |
| PA |
| PB |
A、
| ||||||||
B、1-
| ||||||||
C、
| ||||||||
D、1-
|
，若
，则实数λ的取值范围是（ ） 
≤λ≤1 B.1-
≤λ≤1
≤λ≤1+
D.1-
≤λ≤1+
，若
，则实数λ的取值范围是（ ）
