题目内容
【题目】已知等差数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() 成等比数列,且
成等比数列,且![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)求数列![]() 的前
的前![]() 项和;
项和;
(3)若![]() ,
,![]() 为数列
为数列![]() 的前
的前![]() 项和.若对于任意的
项和.若对于任意的![]() ,都有
,都有![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2) ;(3)
;(3)![]()
【解析】
(1)设等差数列![]() 的公差为
的公差为![]() ,利用等差数列的通项公式以及前
,利用等差数列的通项公式以及前![]() 项和的公式求出
项和的公式求出![]() ,代入通项公式即可.
,代入通项公式即可.
(2)判断出数列![]() 从第六项为负,分类讨论:当
从第六项为负,分类讨论:当![]() 时或当
时或当![]() 时,利用等差数列前
时,利用等差数列前![]() 项和公式即可求解.
项和公式即可求解.
(3)利用裂项求和法求出数列![]() 的前
的前![]() 项和
项和![]() ,
,![]() 恒成立,转化为
恒成立,转化为![]() ,利用单调性求出
,利用单调性求出![]() 的最大值即可.
的最大值即可.
(1)令等差数列![]() 的公差为
的公差为![]() .
.
由于![]() 成等比数列,所以
成等比数列,所以![]() ,
,
又![]() ,所以
,所以![]() ,所以
,所以![]() .
.
(2)记数列![]() 的前
的前![]() 项和为
项和为![]() ,令
,令![]() ,得
,得![]() ,
,
当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]()
![]()
所以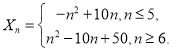
(3)由于![]() ,
,
所以![]() ,
,
由于对于任意的![]() ,都有
,都有![]() 恒成立,所以
恒成立,所以![]() ,
,
当![]() 时,
时,![]() 单调递增,所以当
单调递增,所以当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,所以
,所以![]()
所以![]() ,所以
,所以![]() 的取值范围为
的取值范围为![]() .
.

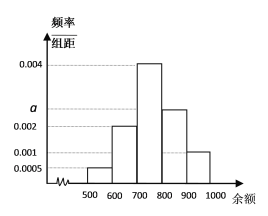
【题目】2018年9月,台风“山竹”在沿海地区登陆,小张调查了当地某小区的100户居民由于台风造成的经济损失,将收集到的数据分成五组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 单位:千元
单位:千元![]() ,并作出如下频率分布直方图
,并作出如下频率分布直方图

经济损失不超过4千元 | 经济损失超过4千元 | 合计 | |
捐款超过 500元 | 60 | ||
捐款不超 过500元 | 10 | ||
合计 |
![]() 1
1![]() 台风后居委会号召小区居民为台风重灾区捐款,小张调查的100户居民捐款情况如表格,在表格空白处填写正确数字,并说明是否有
台风后居委会号召小区居民为台风重灾区捐款,小张调查的100户居民捐款情况如表格,在表格空白处填写正确数字,并说明是否有![]() 以上的把握认为捐款数额多于或少于500元和自身经济损失是否到4千元有关?
以上的把握认为捐款数额多于或少于500元和自身经济损失是否到4千元有关?
![]() 2
2![]() 将上述调查得到的频率视为概率,现在从该地区大量受灾居民中,采用随机抽样的方法每次抽取一户居民,连抽3次,记被抽取的3户居民中自身经济损失超过4千元的户数为
将上述调查得到的频率视为概率,现在从该地区大量受灾居民中,采用随机抽样的方法每次抽取一户居民,连抽3次,记被抽取的3户居民中自身经济损失超过4千元的户数为![]() ,若每次抽取的结果是相互独立的,求
,若每次抽取的结果是相互独立的,求![]() 的分布列和数学期望.
的分布列和数学期望.
附:临界值表:
|
|
|
|
k |
|
|
|
随机变量:![]() ,其中
,其中![]() .
.
【题目】针对“中学生追星问题”,某校团委对“学生性别和中学生追星是否有关”作了一次调查,其中女生人数是男生人数的![]() ,男生追星的人数占男生人数的
,男生追星的人数占男生人数的![]() ,女生追星的人数占女生人数的
,女生追星的人数占女生人数的![]() .若有
.若有![]() 的把握认为是否追星和性别有关,则男生至少有( )
的把握认为是否追星和性别有关,则男生至少有( )
参考数据及公式如下:
|
|
|
|
|
|
|
|
![]()
A. 12B. 11C. 10D. 18
【题目】某快递公司收取快递费用的标准是:重量不超过![]() 的包裹收费
的包裹收费![]() 元;重量超过
元;重量超过![]() 的包裹,除
的包裹,除![]() 收费
收费![]() 元之外,超过
元之外,超过![]() 的部分,每超出
的部分,每超出![]() (不足
(不足![]() ,按
,按![]() 计算)需再收
计算)需再收![]() 元.
元.
该公司将近![]() 天,每天揽件数量统计如下:
天,每天揽件数量统计如下:
包裹件数范围 |
|
|
|
|
|
包裹件数 (近似处理) |
|
|
|
|
|
天数 |
|
|
|
|
|
(1)某人打算将![]() ,
, ![]() ,
, ![]() 三件礼物随机分成两个包裹寄出,求该人支付的快递费不超过
三件礼物随机分成两个包裹寄出,求该人支付的快递费不超过![]() 元的概率;
元的概率;
(2)该公司从收取的每件快递的费用中抽取![]() 元作为前台工作人员的工资和公司利润,剩余的作为其他费用.前台工作人员每人每天揽件不超过
元作为前台工作人员的工资和公司利润,剩余的作为其他费用.前台工作人员每人每天揽件不超过![]() 件,工资
件,工资![]() 元,目前前台有工作人员
元,目前前台有工作人员![]() 人,那么,公司将前台工作人员裁员
人,那么,公司将前台工作人员裁员![]() 人对提高公司利润是否更有利?
人对提高公司利润是否更有利?