题目内容
已知整数数列{an}满足an=an-1-an-2(n≥3),如果前1492项的和是1985,而前1985项的和为1492,则前2001项的和是 .
【答案】分析:我们把数列 看成正整数集 为定义域的函数,则f(n)=f(n-1)-f(n-2),往下推可以求出f(x)的周期,利用递推公式进行求解;
解答:解:定义函数an=f(n),则f(n)=f(n-1)-f(n-2),即可得
f(n)=[f(n-2)-f(n-3)]-f(n-2)=-f(n-3)=-(f(n-4)-f(n-5))=f(n-6),
所以函数an=f(n)是一个周期为6的数列,
设Sn是{an}前n项和,有递推公式可得Sn=an-1+a2
所以S1942=a1491+a2=a3+a2=1985,
S1985=a1984+a2=a4+a2=1492=a3-a2+a2,
∴a2=493,S2001=a2000+a2=a2+a2=986,
故答案为986;
点评:在高考试题中,数列是必考内容,如果我们用函数的观点来看数列,用函数的性质来研究数列可以给我们提供新的思路,优化问题的解答,往往会起到意想不到的效果.
解答:解:定义函数an=f(n),则f(n)=f(n-1)-f(n-2),即可得
f(n)=[f(n-2)-f(n-3)]-f(n-2)=-f(n-3)=-(f(n-4)-f(n-5))=f(n-6),
所以函数an=f(n)是一个周期为6的数列,
设Sn是{an}前n项和,有递推公式可得Sn=an-1+a2
所以S1942=a1491+a2=a3+a2=1985,
S1985=a1984+a2=a4+a2=1492=a3-a2+a2,
∴a2=493,S2001=a2000+a2=a2+a2=986,
故答案为986;
点评:在高考试题中,数列是必考内容,如果我们用函数的观点来看数列,用函数的性质来研究数列可以给我们提供新的思路,优化问题的解答,往往会起到意想不到的效果.

练习册系列答案
相关题目


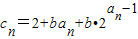 (b为大于等于3的正整数),问数列{cn}中是否存在连续三项成等比数列?若存在,求出所有成等比数列的连续三项;若不存在,请说明理由.
(b为大于等于3的正整数),问数列{cn}中是否存在连续三项成等比数列?若存在,求出所有成等比数列的连续三项;若不存在,请说明理由.
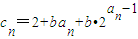 (b为大于等于3的正整数),问数列{cn}中是否存在连续三项成等比数列?若存在,求出所有成等比数列的连续三项;若不存在,请说明理由.
(b为大于等于3的正整数),问数列{cn}中是否存在连续三项成等比数列?若存在,求出所有成等比数列的连续三项;若不存在,请说明理由.