题目内容
已知整数数列{an}满足:a1=1,a2=2,且2an-1<an-1+an+1<2an+1(n∈N,n≥2).(1)求数列{an}的通项公式;
(2)将数列{an}中的所有项依次按如图所示的规律循环地排成如下三角形数表:

…
依次计算各个三角形数表内各行中的各数之和,设由这些和按原来行的前后顺序构成的数列为{bn},求b5+b100的值;
(3)令cn=2+ban+b•2an-1(b为大于等于3的正整数),问数列{cn}中是否存在连续三项成等比数列?若存在,求出所有成等比数列的连续三项;若不存在,请说明理由.
分析:(1)由数列{an}是整数数列,结合2an-1<an-1+an+1<2an+1,可得2an=an-1+an+1,根据等差数列的定义,推出{an}是等差数列,进而求出其通项公式;
(2)仔细读题,找到其循环规律,确定bn是第几个循环中的第几行中各数之和是解题的关键.
(3)由(1)(2)的结论,求出cn的表达式,利用等比数列的定义,得到关于b、n的关系式,然后分n=1,n=2,n≥3分别讨论,即可得出结论.
(2)仔细读题,找到其循环规律,确定bn是第几个循环中的第几行中各数之和是解题的关键.
(3)由(1)(2)的结论,求出cn的表达式,利用等比数列的定义,得到关于b、n的关系式,然后分n=1,n=2,n≥3分别讨论,即可得出结论.
解答:解:(1)因为数列{an}是整数数列,所以an是整数,
所以2an-1,an-1+an+1,2an+1都是整数.
又2an-1<an-1+an+1<2an+1(n∈N,n≥2),
所以2an=an-1+an+1,
即数列{an}是首项为1,公差d=a2-a1=1的等差数列,所以an=n.
(2)设每一个循环(4行)记为一组,由于每一个循环含有4行,
故b100是第25个循环中的第4行中各数之和.
由循环分组规律知,每个循环共有10项,
故第25个循环中的第4行内的4个数分别为数列{an}中的第247项至第250项,
又an=n.所以b100=247+248+249+250=994.
b5=a11=11,所以b5+b100=11+994=1005.
(3)因为cn=2+ban+b•2an-1=2+bn+b•2n-1,
设数列{cn}中,cn,cn+1,cn+2成等比数列,即cn+12=cn•cn+2,
所以(2+nb+b+b•2n)2=(2+nb+b•2n-1)(2+nb+2b+b•2n+1)
化简得b=2n+(n-2)•b•2n-1(*)
当n=1时,b=1,等式(*)成立,而b≥3,故等式(*)不成立;
当n=2时,b=4,等式(*)成立;
当n≥3时,b=2n+(n-2)•b•2n-1>(n-2)•b•2n-1≥4b,这与b≥3矛盾,故等式(*)不成立.
综上所述,当b≠4时,数列{cn}中不存在连续三项等等比数列;
当b=4时,数列{cn}中存在连续三项等等比数列,这三项依次是18,30,50.
所以2an-1,an-1+an+1,2an+1都是整数.
又2an-1<an-1+an+1<2an+1(n∈N,n≥2),
所以2an=an-1+an+1,
即数列{an}是首项为1,公差d=a2-a1=1的等差数列,所以an=n.
(2)设每一个循环(4行)记为一组,由于每一个循环含有4行,
故b100是第25个循环中的第4行中各数之和.
由循环分组规律知,每个循环共有10项,
故第25个循环中的第4行内的4个数分别为数列{an}中的第247项至第250项,
又an=n.所以b100=247+248+249+250=994.
b5=a11=11,所以b5+b100=11+994=1005.
(3)因为cn=2+ban+b•2an-1=2+bn+b•2n-1,
设数列{cn}中,cn,cn+1,cn+2成等比数列,即cn+12=cn•cn+2,
所以(2+nb+b+b•2n)2=(2+nb+b•2n-1)(2+nb+2b+b•2n+1)
化简得b=2n+(n-2)•b•2n-1(*)
当n=1时,b=1,等式(*)成立,而b≥3,故等式(*)不成立;
当n=2时,b=4,等式(*)成立;
当n≥3时,b=2n+(n-2)•b•2n-1>(n-2)•b•2n-1≥4b,这与b≥3矛盾,故等式(*)不成立.
综上所述,当b≠4时,数列{cn}中不存在连续三项等等比数列;
当b=4时,数列{cn}中存在连续三项等等比数列,这三项依次是18,30,50.
点评:本题在应用等差数列的定义、通项公式、前n项和公式的同时,还考查了学生的逻辑推理能力,运算能力以及对公式的灵活运用能力,是一道综合性很强的题目.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目

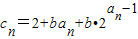 (b为大于等于3的正整数),问数列{cn}中是否存在连续三项成等比数列?若存在,求出所有成等比数列的连续三项;若不存在,请说明理由.
(b为大于等于3的正整数),问数列{cn}中是否存在连续三项成等比数列?若存在,求出所有成等比数列的连续三项;若不存在,请说明理由.
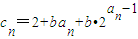 (b为大于等于3的正整数),问数列{cn}中是否存在连续三项成等比数列?若存在,求出所有成等比数列的连续三项;若不存在,请说明理由.
(b为大于等于3的正整数),问数列{cn}中是否存在连续三项成等比数列?若存在,求出所有成等比数列的连续三项;若不存在,请说明理由.