��Ŀ����
��֪��������{an}���㣺a1=1��a2=2����2an-1��an-1+an+1��2an+1��n��N��n��2������1��������{an}��ͨ�ʽ��
��2��������{an}�е����������ΰ���ͼ��ʾ�Ĺ���ѭ�����ų�����������������

��
���μ�����������������ڸ����еĸ���֮�ͣ�������Щ�Ͱ�ԭ���е�ǰ��˳�ɵ�����Ϊ{bn}����b5+b100��ֵ��
��3����
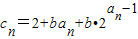 ��bΪ���ڵ���3������������������{cn}���Ƿ������������ɵȱ����У������ڣ�������гɵȱ����е���������������ڣ���˵�����ɣ�
��bΪ���ڵ���3������������������{cn}���Ƿ������������ɵȱ����У������ڣ�������гɵȱ����е���������������ڣ���˵�����ɣ�
���𰸡���������1��������{an}���������У����2an-1��an-1+an+1��2an+1���ɵ�2an=an-1+an+1�����ݵȲ����еĶ��壬�Ƴ�{an}�ǵȲ����У����������ͨ�ʽ��
��2����ϸ���⣬�ҵ���ѭ�����ɣ�ȷ��bn�ǵڼ���ѭ���еĵڼ����и���֮���ǽ���Ĺؼ���
��3���ɣ�1����2���Ľ��ۣ����cn�ı���ʽ�����õȱ����еĶ��壬�õ�����b��n�Ĺ�ϵʽ��Ȼ���n=1��n=2��n��3�ֱ����ۣ����ɵó����ۣ�
����⣺��1����Ϊ����{an}���������У�����an��������
����2an-1��an-1+an+1��2an+1����������
��2an-1��an-1+an+1��2an+1��n��N��n��2����
����2an=an-1+an+1��
������{an}������Ϊ1������d=a2-a1=1�ĵȲ����У�����an=n��
��2����ÿһ��ѭ����4�У���Ϊһ�飬����ÿһ��ѭ������4�У�
��b100�ǵ�25��ѭ���еĵ�4���и���֮�ͣ�
��ѭ���������֪��ÿ��ѭ������10�
�ʵ�25��ѭ���еĵ�4���ڵ�4�����ֱ�Ϊ����{an}�еĵ�247������250�
��an=n������b100=247+248+249+250=994��
b5=a11=11������b5+b100=11+994=1005��
��3����Ϊ ��
��
������{cn}�У�cn��cn+1��cn+2�ɵȱ����У���cn+12=cn•cn+2��
���ԣ�2+nb+b+b•2n��2=��2+nb+b•2n-1����2+nb+2b+b•2n+1��
�����b=2n+��n-2��•b•2n-1��*��
��n=1ʱ��b=1����ʽ��*����������b��3���ʵ�ʽ��*����������
��n=2ʱ��b=4����ʽ��*��������
��n��3ʱ��b=2n+��n-2��•b•2n-1����n-2��•b•2n-1��4b������b��3ì�ܣ��ʵ�ʽ��*����������
������������b��4ʱ������{cn}�в�������������ȵȱ����У�
��b=4ʱ������{cn}�д�����������ȵȱ����У�������������18��30��50��
������������Ӧ�õȲ����еĶ��塢ͨ�ʽ��ǰn���ʽ��ͬʱ����������ѧ�������������������������Լ��Թ�ʽ�����������������һ���ۺ��Ժ�ǿ����Ŀ��
��2����ϸ���⣬�ҵ���ѭ�����ɣ�ȷ��bn�ǵڼ���ѭ���еĵڼ����и���֮���ǽ���Ĺؼ���
��3���ɣ�1����2���Ľ��ۣ����cn�ı���ʽ�����õȱ����еĶ��壬�õ�����b��n�Ĺ�ϵʽ��Ȼ���n=1��n=2��n��3�ֱ����ۣ����ɵó����ۣ�
����⣺��1����Ϊ����{an}���������У�����an��������
����2an-1��an-1+an+1��2an+1����������
��2an-1��an-1+an+1��2an+1��n��N��n��2����
����2an=an-1+an+1��
������{an}������Ϊ1������d=a2-a1=1�ĵȲ����У�����an=n��
��2����ÿһ��ѭ����4�У���Ϊһ�飬����ÿһ��ѭ������4�У�
��b100�ǵ�25��ѭ���еĵ�4���и���֮�ͣ�
��ѭ���������֪��ÿ��ѭ������10�
�ʵ�25��ѭ���еĵ�4���ڵ�4�����ֱ�Ϊ����{an}�еĵ�247������250�
��an=n������b100=247+248+249+250=994��
b5=a11=11������b5+b100=11+994=1005��
��3����Ϊ
 ��
��������{cn}�У�cn��cn+1��cn+2�ɵȱ����У���cn+12=cn•cn+2��
���ԣ�2+nb+b+b•2n��2=��2+nb+b•2n-1����2+nb+2b+b•2n+1��
�����b=2n+��n-2��•b•2n-1��*��
��n=1ʱ��b=1����ʽ��*����������b��3���ʵ�ʽ��*����������
��n=2ʱ��b=4����ʽ��*��������
��n��3ʱ��b=2n+��n-2��•b•2n-1����n-2��•b•2n-1��4b������b��3ì�ܣ��ʵ�ʽ��*����������
������������b��4ʱ������{cn}�в�������������ȵȱ����У�
��b=4ʱ������{cn}�д�����������ȵȱ����У�������������18��30��50��
������������Ӧ�õȲ����еĶ��塢ͨ�ʽ��ǰn���ʽ��ͬʱ����������ѧ�������������������������Լ��Թ�ʽ�����������������һ���ۺ��Ժ�ǿ����Ŀ��

��ϰ��ϵ�д�
�����Ŀ


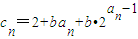 ��bΪ���ڵ���3������������������{cn}���Ƿ������������ɵȱ����У������ڣ�������гɵȱ����е���������������ڣ���˵�����ɣ�
��bΪ���ڵ���3������������������{cn}���Ƿ������������ɵȱ����У������ڣ�������гɵȱ����е���������������ڣ���˵�����ɣ�