题目内容
【题目】为响应国家“精准扶贫，产业扶贫“的战略，进一步优化能源消费结构，某市决定在一地处山区的
县推进光伏发电项目，在该县山区居民中随机抽取50户，统计其年用电量得到以下统计表，以样本的频率作为概率．
用电量（度） |
|
|
|
|
|
户数 | 5 | 15 | 10 | 15 | 5 |
（1）在该县山区居民中随机抽取10户，记其中年用电量不超过600度的户数为
，求
的数学期望；
（2）已知该县某山区自然村有居民300户，若计划在该村安装总装机容量为300千瓦的光伏发电机组，该机组所发电量除保证该村正常用电外，剩余电量国家电网以
元/度进行收购．经测算以每千瓦装机容量平均发电1000度，试估计该机组每年所发电量除保证正常用电外还能为该村创造直接收益多少元？
【答案】（1）6（2）120000
【解析】
试题分析：（1）先判断随机变量服从二项分布，所以求数学期望的关键为求概率：由频率估计概率得
，最后根据二项分布数学期望公式得
（2）按数学期望计算平均每户正常用电量：
，进而可得全村年均用电量约150000度．剩余电量约300000-150000=150000，收益
试题解析：（1）记在该县山区居民中随机抽取1户，其年用电量不超过600度为事件
．
由抽样可知，
．．．．．．．．．．．．．．．．．．．．．．．．．．3分
由已知可得从该县山区居民中随机抽取10户，记其中年用电量不超过600度的户数
，服从二项分布，即
，故．．．．．．．．．．．．．．．．．．．．6分
（2）设该县山区居民户年均用电量为
，由抽样可得
（度）．．．．．．．．．．．．10分
则该自然村年均用电约150000度．
又该村所装发电机组年预计发电量为300000度，故该机组每年所发电量除保证正常用电外还能剩余电量约150000度，能为该村创造直接收益120000元．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．12分
【题目】为做好2022年北京冬季奥运会的宣传工作，组委会计划从某大学选取若干大学生志愿者，某记者在该大学随机调查了300名大学生，以了解他们是否愿意做志愿者工作，得到的数据如表所示：
愿意做志愿者工作 | 不愿意做志愿者工作 | 合计 | |
男大学生 | 180 | ||
女大学生 | 45 | ||
合计 | 200 |
（Ⅰ）根据题意完成表格；
（Ⅱ）是否有
的把握认为愿意做志愿者工作与性别有关？
附：
，
| 0.5 | 0.40 | 0.25 | 0.15 | 0.10 |
| 0.455 | 0.708 | 1.323 | .072 | 2.706 |
【题目】为研究冬季昼夜温差大小对某反季节大豆新品种发芽率的影响，某农科所记录了5组昼夜温差与100颗种子发芽数，得到如下资料：
组号 | 1 | 2 | 3 | 4 | 5 |
温差 | 10 | 11 | 13 | 12 | 8 |
发芽数 | 23 | 25 | 30 | 26 | 16 |
该所确定的研究方案是：先从这五组数据中选取2组，用剩下的3组数据求出线性回归方程，再对被选取的2组数据进行检验．
（1）若选取的是第1组与第5组的两组数据，请根据第2组至第4组的数据，求出
关于
的线性回归方程
；
（2）若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2颗，则认为得到的线性回归方程是可靠的，试问（1）中所得的线性回归方程是否可靠？
（参考公式：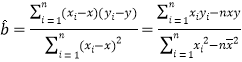
，
）
【题目】某市2010年至2016年新开楼盘的平均销售价格
（单位：千元/平米）的统计数据如下表：
年份 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 |
年份代号x | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
销售价格y | 3 | 3.4 | 3.7 | 4.5 | 4.9 | 5.3 | 6 |
（1）求
关于
的线性回归方程；
（2）利用（1）中的回归方程，分析2010年至2016年该市新开楼盘平均销售价格的变化情况，并预测该市2018年新开楼盘的平均销售价格.
附：参考数据及公式： 
， 
， 
.
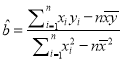