题目内容
【题目】随着通识教育理念的推广及高校课程改革的深入，选修课越来越受到人们的重视.国内一些知名院校在公共选修课的设置方面做了许多有益的探索，并且取得了一定的成果.因为选修课的课程建设处于探索阶段，选修课的教学、管理还存在很多的问题，所以需要在通识教育的基础上制定科学的、可行的解决方案，为学校选修课程的改革与创新、课程设置、考试考核、人才培养提供参考.某高校采用分层抽样法抽取了数学专业的50名参加选修课与不参加选修课的学生的成绩，统计数据如下表：
成绩优秀 | 成绩不够优秀 | 总计 | |
参加选修课 | 16 | 9 | 25 |
不参加选修课 | 8 | 17 | 25 |
总计 | 24 | 26 | 50 |
（1）试运用独立性检验的思想方法你能否有99%的把握认为“学生的成绩优秀与是否参加选修课有关”，并说明理由；
（2）如果从数学专业随机抽取5名学生，求抽到参加选修课的学生人数
的分布列和数学期望（将频率当做概率计算）.
参考公式：
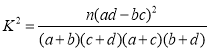，其中
.
临界值表：
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【答案】（1）没有99%的把握认为“学生的成绩优秀与是否参加选修课有关；（2）分布列见解析，
【解析】
（1）由卡方公式计算
，再与临界值表对照可得结论；
（2）由题意知，数学专业中参加选修课的学生的概率为
.随机抽取5名学生，抽到参加选修课的学生人数的所有可能取值为0，1，2，3，4，5，利用二项分布的概率公式可计算出概率得分布列，由期望公式可求得期望．
（1）由题意知，
.
没有99%的把握认为“学生的成绩优秀与是否参加选修课有关”
（2）由题意知，数学专业中参加选修课的学生的概率为.
随机抽取5名学生，抽到参加选修课的学生人数的所有可能取值为0，1，2，3，4，5.
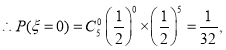
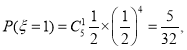
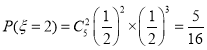
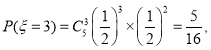
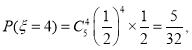
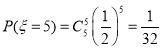
的分布列为
| 0 | 1 | 2 | 3 | 4 | 5 |
P |
|
|
|
|
|
|
