题目内容
对任意的实数a,b,记max{a,b}=
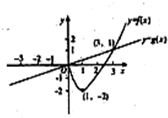
,若F(x)=max{f(x),g(x)}(x∈R),其中奇函数y=f(x)在x=1时有极小值-2,y=g(x)是正比例函数,函数y=f(x)(x≥0)与函数y=g(x)的图象如图所示,则下列关于函数y=F(x)的说法中,正确的是( )
|
| A.y=F(x)为奇函数 |
| B.y=F(x)有极大值F(1)且有极小值F(-1) |
| C.y=F(x)在(-3,0)上不是单调函数 |
| D.y=F(x)的最小值为-2且最大值为2 |

由图象可得g(x)=
x;
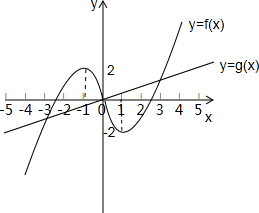
根据当x≥0时,由f(x)的图象和奇函数y=f(x)在x=1时有极小值-2,可知:当x≤0时,在x=-1时取得最大值2,及其f(x)的图象如图所示.
而F(x)=
,
因此当-3≤x≤0时,函数F(x)不单调.
故选C.
| 1 |
| 3 |

根据当x≥0时,由f(x)的图象和奇函数y=f(x)在x=1时有极小值-2,可知:当x≤0时,在x=-1时取得最大值2,及其f(x)的图象如图所示.
而F(x)=
|
因此当-3≤x≤0时,函数F(x)不单调.
故选C.

练习册系列答案
 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案 小学学习好帮手系列答案
小学学习好帮手系列答案
相关题目
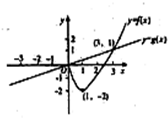 (2011•烟台一模)对任意的实数a,b,记max{a,b}=
(2011•烟台一模)对任意的实数a,b,记max{a,b}=