Question

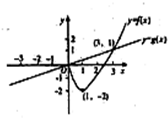（2011•烟台一模）对任意的实数a，b，记max{a，b}=

a(a≥b) b(a＜b)

，若F（x）=max{f（x），g（x）}（x∈R），其中奇函数y=f（x）在x=1时有极小值-2，y=g（x）是正比例函数，函数y=f（x）（x≥0）与函数y=g（x）的图象如图所示，则下列关于函数y=F（x）的说法中，正确的是（　　）

A．y=F（x）为奇函数

B．y=F（x）有极大值F（1）且有极小值F（-1）

C．y=F（x）在（-3，0）上不是单调函数

D．y=F（x）的最小值为-2且最大值为2

Answer 1

分析：利用奇函数的性质和新定义即可得出．

解答：解：由图象可得g（x）=

1

3

x；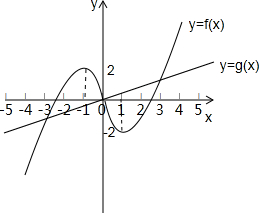
根据当x≥0时，由f（x）的图象和奇函数y=f（x）在x=1时有极小值-2，可知：当x≤0时，在x=-1时取得最大值2，及其f（x）的图象如图所示．
而F（x）=

f(x)，-3≤x≤0或x≥3 g(x)，x＜-3或0＜x＜3

，
因此当-3≤x≤0时，函数F（x）不单调．
故选C．

点评：正确理解奇函数的性质和新定义是解题的关键．