题目内容
(2011•丰台区一模)已知点A(-1,0),B(1,0),动点P满足|PA|+|PB|=2
,记动点P的轨迹为W.
(Ⅰ)求W的方程;
(Ⅱ)直线y=kx+1与曲线W交于不同的两点C,D,若存在点M(m,0),使得|CM|=|DM|成立,求实数m的取值范围.
| 3 |
(Ⅰ)求W的方程;
(Ⅱ)直线y=kx+1与曲线W交于不同的两点C,D,若存在点M(m,0),使得|CM|=|DM|成立,求实数m的取值范围.
分析:(Ⅰ)依题意,点P到两定点A、B的距离之和为定值2
,且此值大于两定点间的距离2,由椭圆定义可知动点P的轨迹是以A,B为焦点,长轴长为2
的椭圆,从而写出W的标准方程
(Ⅱ)先将直线方程与曲线W的方程联立,得关于x的一元二次方程,利用韦达定理,写出交点C、D的横坐标的和与积,再求出线段CD的中垂线的方程,此直线与x轴的交点即为M,从而得m关于k的函数,求函数值域即可
| 3 |
| 3 |
(Ⅱ)先将直线方程与曲线W的方程联立,得关于x的一元二次方程,利用韦达定理,写出交点C、D的横坐标的和与积,再求出线段CD的中垂线的方程,此直线与x轴的交点即为M,从而得m关于k的函数,求函数值域即可
解答:解:(Ⅰ)∵|PA|+|PB|=2
>|AB|=2
∴由椭圆的定义可知,动点P的轨迹是以A,B为焦点,长轴长为2
的椭圆.
∴c=1,a=
,b2=2.
∴W的方程是
+
=1.
(Ⅱ)设C,D两点坐标分别为C(x1,y1)、D(x2,y2),C,D中点为N(x0,y0).
由
得 (3k2+2)x2+6kx-3=0.
∵△=36k2+12(3k2+2)>0
∴x1+x2=-
,
∴x0=
=-
,从而y0=kx0+1=
.
∴线段CD的中垂线的方程为y-y0=-
(x-x0)
即y-
=-
(x+
)
令y=0,得x=--
∵存在点M(m,0),使得|CM|=|DM|
∴m=-
当k=0时,m=0
当k>0时,m=-
=-
≥-
=-
即m∈[-
,0)
当k<0时,m=-
=-
≤
=
即m∈(0,
]
∴m∈[-
,0)∪(0,
]∪{0}=[-
,
].
故所求m的取范围是[-
,
].
| 3 |
∴由椭圆的定义可知,动点P的轨迹是以A,B为焦点,长轴长为2
| 3 |
∴c=1,a=
| 3 |
∴W的方程是
| x2 |
| 3 |
| y2 |
| 2 |
(Ⅱ)设C,D两点坐标分别为C(x1,y1)、D(x2,y2),C,D中点为N(x0,y0).
由
|
∵△=36k2+12(3k2+2)>0
∴x1+x2=-
| 6k |
| 3k2+2 |
∴x0=
| x1+x2 |
| 2 |
| 3k |
| 3k2+2 |
| 2 |
| 3k2+2 |
∴线段CD的中垂线的方程为y-y0=-
| 1 |
| k |
即y-
| 2 |
| 3k2+2 |
| 1 |
| k |
| 3k |
| 3k2+2 |
令y=0,得x=--
| k |
| 3k2+2 |
∵存在点M(m,0),使得|CM|=|DM|
∴m=-
| k |
| 3k2+2 |
当k=0时,m=0
当k>0时,m=-
| k |
| 3k2+2 |
| 1 | ||
3k+
|
| 1 | ||||
2
|
| ||
| 12 |
即m∈[-
| ||
| 12 |
当k<0时,m=-
| k |
| 3k2+2 |
| 1 | ||
3k+
|
| 1 | ||||
2
|
| ||
| 12 |
即m∈(0,
| ||
| 12 |
∴m∈[-
| ||
| 12 |
| ||
| 12 |
| ||
| 12 |
| ||
| 12 |
故所求m的取范围是[-
| ||
| 12 |
| ||
| 12 |
点评:本题考查了椭圆的定义及椭圆的标准方程,直线与椭圆的位置关系,特别是直线与椭圆相交时,利用韦达定理设而不求的技巧解决几何问题,是本题考查的重点

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
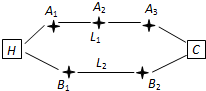 (2011•丰台区二模)张先生家住H小区,他在C科技园区工作,从家开车到公司上班有L1,L2两条路线(如图),L1路线上有A1,A2,A3三个路口,各路口遇到红灯的概率均为
(2011•丰台区二模)张先生家住H小区,他在C科技园区工作,从家开车到公司上班有L1,L2两条路线(如图),L1路线上有A1,A2,A3三个路口,各路口遇到红灯的概率均为