题目内容

（2011•丰台区一模）已知圆M：x2+y2-2x-4y+1=0，则圆心M到直线
x=4t+3
y=3t+1
（t为参数）的距离为
2
2
．
分析：把圆的方程化为标准方程后，找出圆心坐标，把直线的参数方程化为普通方程后，利用点到直线的距离公式即可求出圆心M到已知直线的距离．
解答：解：把圆M的方程化为标准方程得：（x-1）2+（y-2）2=4，
得到圆心M的坐标为（1，2），
由直线的参数方程化为普通方程得：3x-4y-5=0，
则圆心M到直线的距离d=
|3-8-5|
32+42
=2．
故答案为：2
点评：此题考查学生会将直线的参数方程化为普通方程及圆的一般方程化为标准方程，灵活运用点到直线的距离公式化简求值，是一道基础题．
练习册系列答案
相关题目
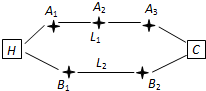（2011•丰台区二模）张先生家住H小区，他在C科技园区工作，从家开车到公司上班有L1，L2两条路线（如图），L1路线上有A1，A2，A3三个路口，各路口遇到红灯的概率均为
1
2
；L2路线上有B1，B2两个路口，各路口遇到红灯的概率依次为
3
4
，
3
5
．
（Ⅰ）若走L1路线，求最多遇到1次红灯的概率；
（Ⅱ）若走L2路线，求遇到红灯次数X的数学期望；
（Ⅲ）按照“平均遇到红灯次数最少”的要求，请你帮助张先生从上述两条路线中选择一条最好的上班路线，并说明理由．
关于概率统计问题，几次考查都没有将概率与统计图表结合起来，请老师们注意，在复练时要有意识的进行练习．
（2011•丰台区一模）已知点A（-1，0），B（1，0），动点P满足|PA|+|PB|=2
3
，记动点P的轨迹为W．
（Ⅰ）求W的方程；  
（Ⅱ）直线y=kx+1与曲线W交于不同的两点C，D，若存在点M（m，0），使得|CM|=|DM|成立，求实数m的取值范围．
（2011•丰台区一模）已知函数f（x）=
x3，x≤0
1n(x+1)，x＞0
，若则实数x的取值范围是（　　）

（2011•丰台区一模）将全体正奇数排成一个三角形数阵：
1
3   5
7   9   11
13  15  17  19
…
按照以上排列的规律，第n 行（n≥3）从左向右的第3个数为　       　．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网