题目内容
4.用符号(x]表示不小于x的最小整数,如(π]=4,(-1.2]=-1.则方程(x]-x=$\frac{1}{2}$在(1,4)上实数解的个数为( )| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 根据定义分别讨论x的取值范围,解方程即可.
解答 解:若1<x≤2,则(x]=2,由(x]-x=$\frac{1}{2}$得2-x=$\frac{1}{2}$,即x=$\frac{3}{2}$,
若2<x≤3,则(x]=3,由(x]-x=$\frac{1}{2}$得3-x=$\frac{1}{2}$,即x=$\frac{5}{2}$,
若3<x<4,则(x]=4,由(x]-x=$\frac{1}{2}$得4-x=$\frac{1}{2}$,即x=$\frac{7}{2}$,
故方程(x]-x=$\frac{1}{2}$在(1,4)上实数解的个数为3个,
故选:D.
点评 本题主要考查方程根的个数的判断,根据定义利用分类讨论是解决本题的关键.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
14.某流程图如图所示,现输入如下四个函数,则可以输出f(x)的是( )
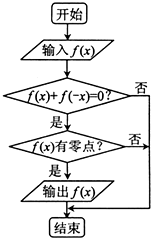

| A. | f(x)=-x2+1 | B. | f(x)=x+$\frac{1}{x}$ | C. | f(x)=lg$\frac{1+x}{1-x}$ | D. | f(x)=$\frac{{2}^{x}+1}{{2}^{x}-1}$ |
15.已知过点A(1,m)恰能作曲线f(x)=x3-3x的两条切线,则m的值是( )
| A. | -1 | B. | -2 | C. | -3 | D. | -3或-2 |
12.有3个学习兴趣小组,甲、乙两位同学各自参加其中一个小组,每位同学参加各个小组的可能性相同,则这两位同学参加同一个兴趣小组的概率为( )
| A. | $\frac{3}{4}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{3}$ |
13.定义在R上的偶函数f(x)满足f(x+1)=-f(x),且在[-5,-4]上是减函数,α、β是锐角三角形的两个内角,则( )
| A. | f(sinα)>f(cosβ) | B. | f(sinα)>f(sinβ) | C. | f(sinα)<f(cosβ) | D. | f(cosα)>f(cosβ) |
14.在一项吃零食与性别的调查中,运用2×2列联表进行独立性检验得到K2≈2.521,那么判断吃零食和性别有关的这种判断的出错率为( )
| A. | 1% | B. | 99% | C. | 15% | D. | 90% |