题目内容
（2012•虹口区三模）设连续掷两次骰子得到的点数分别为m，n（m，n=1，2，…，6），则直线y=
x与圆（x-3）2+y2=1相交的概率是
．
| m |
| n |
| 5 |
| 36 |
| 5 |
| 36 |
分析：先研究出直线与圆相交的条件，再依据条件找出符合条件的点数m，n的组数，以及直线的总个数．
解答：解：直线y=
x 与圆（x-3）2+y2=1相交时，直线的斜率小于
，
考虑到m、n为正整数，应使直线的斜率小于或等于
，
当m=1时，n=3，4，5，6，
当m=2时，n=6，共有5种情况，其概率为
，
故答案为
．
| m |
| n |
| ||
| 4 |
考虑到m、n为正整数，应使直线的斜率小于或等于
| 1 |
| 3 |
当m=1时，n=3，4，5，6，
当m=2时，n=6，共有5种情况，其概率为
| 5 |
| 36 |
故答案为
| 5 |
| 36 |
点评：题考查直线与圆的位置关系，本题是创新型题由骰子为背景，结合概率，考法新颖，属于中档题．
练习册系列答案
全优考典单元检测卷及归类总复习系列答案
品学双优卷系列答案
相关题目
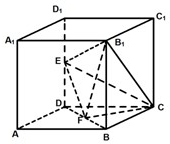（2012•虹口区三模）如图所示，在棱长为2的正方体ABCD-A1B1C1D1中，E、F分别为DD1、DB的中点．
（2012•虹口区三模）函数y=2x和y=x3的图象的示意图如图所示，设两函数的图象交于点A（x1，y1），B（x2，y2），且x1＜x2．