��Ŀ����
��2012•�������ģ����֪����{an}����a1=2��an+1=2(1+
)2an��
��1����bn=
��������{bn}��{an}��ͨ�ʽ��
��2����cn=(An2+Bn+C)•2n�����ƶ��Ƿ���ڳ���A��B��C��ʹ��һ��n��N*����an=cn+1-cn�����������ڣ����A��B��C��ֵ���������ڣ�˵�����ɣ�
��3���ԣ�2��������{cn}����dn=
����{dn}����С���ֵ��
| 1 |
| n |
��1����bn=
| an |
| n2 |
��2����cn=(An2+Bn+C)•2n�����ƶ��Ƿ���ڳ���A��B��C��ʹ��һ��n��N*����an=cn+1-cn�����������ڣ����A��B��C��ֵ���������ڣ�˵�����ɣ�
��3���ԣ�2��������{cn}����dn=
| an |
| cn |
��������1�����������ɵ�
=2•
���Ӷ��ɵ�{bn}�ǹ���Ϊ2�ĵȱ����У��ɴ˿�������{bn}��{an}��ͨ�ʽ��
��2������cn=(An2+Bn+C)•2n���������an=cn+1-cn��������ɵ�An2+��4A+B��n+2A+2B+C=n2��������ɴ˿���A��B��C��ֵ��
��3����dn=
=
����t=
��(0��1]�������䷽����������ý��ۣ�
| an+1 |
| (n+1)2 |
| an |
| n2 |
��2������cn=(An2+Bn+C)•2n���������an=cn+1-cn��������ɵ�An2+��4A+B��n+2A+2B+C=n2��������ɴ˿���A��B��C��ֵ��
��3����dn=
| n2 |
| n2-4n+6 |
| 1 | ||||
|
| 1 |
| n |
����⣺��1������֪��
=2•
����{bn}�ǹ���Ϊ2�ĵȱ����У�
��b1=2����bn=2•2n-1=2n
��bn=
=2•2n-1=2n����an=2n•n2
��2����cn=(An2+Bn+C)•2n��
��cn+1-cn=[A(n+1)2+B(n+1)+C]•2n+1-(An2+Bn+C)•2n=[An2+��4A+B��n+2A+2B+C]•2n
��an=cn+1-cn���������An2+��4A+B��n+2A+2B+C=n2�������
��
����A=1��B=-4��C=6
�ʴ��ڳ���A=1��B=-4��C=6��������
��3��dn=
=
����t=
��(0��1]
��
-
+1=6t2-4t+1=6(t-
)2+
��t�ʣ�0��1]����t=1ʱ��
-
+1=6t2-4t+1�����ֵΪ3
��{dn}����С���ֵΪ
| an+1 |
| (n+1)2 |
| an |
| n2 |
��b1=2����bn=2•2n-1=2n
��bn=
| an |
| n2 |
��2����cn=(An2+Bn+C)•2n��
��cn+1-cn=[A(n+1)2+B(n+1)+C]•2n+1-(An2+Bn+C)•2n=[An2+��4A+B��n+2A+2B+C]•2n
��an=cn+1-cn���������An2+��4A+B��n+2A+2B+C=n2�������
��
|
�ʴ��ڳ���A=1��B=-4��C=6��������
��3��dn=
| n2 |
| n2-4n+6 |
| 1 | ||||
|
| 1 |
| n |
��
| 6 |
| n2 |
| 4 |
| n |
| 1 |
| 3 |
| 1 |
| 3 |
��t�ʣ�0��1]����t=1ʱ��
| 6 |
| n2 |
| 4 |
| n |
��{dn}����С���ֵΪ
| 1 |
| 3 |
���������⿼��ȱ����е�֤����������ʽ��������������ֵ����ȷ��������ͨ���ǹؼ���

��ϰ��ϵ�д�
�����Ŀ
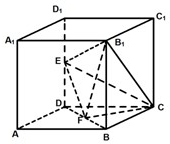 ��2012•�������ģ����ͼ��ʾ�����ⳤΪ2��������ABCD-A1B1C1D1�У�E��F�ֱ�ΪDD1��DB���е㣮
��2012•�������ģ����ͼ��ʾ�����ⳤΪ2��������ABCD-A1B1C1D1�У�E��F�ֱ�ΪDD1��DB���е㣮 ��2012•�������ģ������y=2x��y=x3��ͼ���ʾ��ͼ��ͼ��ʾ������������ͼ���ڵ�A��x1��y1����B��x2��y2������x1��x2��
��2012•�������ģ������y=2x��y=x3��ͼ���ʾ��ͼ��ͼ��ʾ������������ͼ���ڵ�A��x1��y1����B��x2��y2������x1��x2��