题目内容
(2012•虹口区三模)数列{an}满足:an=
且{an}是递增数列,则实数a的范围是( )
|
分析:根据题意,首先可得an通项公式,这是一个类似与分段函数的通项,结合分段函数的单调性的判断方法,可得
;解可得答案.
|
解答: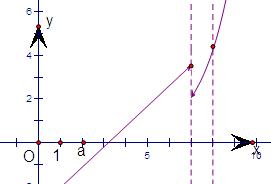 解:根据题意,an=f(n)=
解:根据题意,an=f(n)=
;
要使{an}是递增数列,必有
;
解可得,2<a<3;
故选D.
 解:根据题意,an=f(n)=
解:根据题意,an=f(n)=
|
要使{an}是递增数列,必有
|
解可得,2<a<3;
故选D.
点评:本题考查分段函数的解析式求法及其图象的作法、数列的函数特性、函数单调性的判断与证明,{an}是递增数列,必须结合f(x)的单调性进行解题,但要注意{an}是递增数列与f(x)是增函数的区别与联系.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
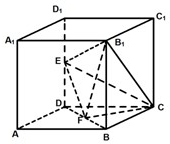 (2012•虹口区三模)如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E、F分别为DD1、DB的中点.
(2012•虹口区三模)如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E、F分别为DD1、DB的中点. (2012•虹口区三模)函数y=2x和y=x3的图象的示意图如图所示,设两函数的图象交于点A(x1,y1),B(x2,y2),且x1<x2.
(2012•虹口区三模)函数y=2x和y=x3的图象的示意图如图所示,设两函数的图象交于点A(x1,y1),B(x2,y2),且x1<x2.