题目内容
 (2012•虹口区三模)函数y=2x和y=x3的图象的示意图如图所示,设两函数的图象交于点A(x1,y1),B(x2,y2),且x1<x2.
(2012•虹口区三模)函数y=2x和y=x3的图象的示意图如图所示,设两函数的图象交于点A(x1,y1),B(x2,y2),且x1<x2.(1)设曲线C1,C2分别对应函数y=f(x)和y=g(x),请指出图中曲线C1,C2对应的函数解析式.若不等式kf[g(x)]-g(x)<0对任意x∈(0,1)恒成立,求k的取值范围;
(2)若x1∈[a,a+1],x2∈[b,b+1],且a,b∈{1,2,3,4,5,6,7,8,9,10,11,12},求a,b的值.
分析:(1)由题意,C1对应的函数为f(x)=x3,C2对应的函数为g(x)=2x ,不等式kf[g(x)]-g(x)<0,等价于k•23x<2x,利用分离参数法,可求k的取值范围;
(2)令φ(x)=g(x)-f(x)=2x-x3,则x1,x2为函数φ(x)的零点,根据零点存在定理,可得两个零点x1∈(1,2),x2∈(9,10),由此可得a,b的值.
(2)令φ(x)=g(x)-f(x)=2x-x3,则x1,x2为函数φ(x)的零点,根据零点存在定理,可得两个零点x1∈(1,2),x2∈(9,10),由此可得a,b的值.
解答:解:(1)由题意,C1对应的函数为f(x)=x3,C2对应的函数为g(x)=2x
不等式kf[g(x)]-g(x)<0,等价于k•23x<2x,则k<4-x对任意x∈(0,1)恒成立(4分)
∵4-x∈(
,1),∴k≤
(2)令φ(x)=g(x)-f(x)=2x-x3,则x1,x2为函数φ(x)的零点,
由于φ(1)=1>0,φ(2)=-4<0,φ(9)=29-93<0,φ(10)=210-103>0,
则方程φ(x)=f(x)-g(x)的两个零点x1∈(1,2),x2∈(9,10),
因此整数a=1,b=9.
不等式kf[g(x)]-g(x)<0,等价于k•23x<2x,则k<4-x对任意x∈(0,1)恒成立(4分)
∵4-x∈(
| 1 |
| 4 |
| 1 |
| 4 |
(2)令φ(x)=g(x)-f(x)=2x-x3,则x1,x2为函数φ(x)的零点,
由于φ(1)=1>0,φ(2)=-4<0,φ(9)=29-93<0,φ(10)=210-103>0,
则方程φ(x)=f(x)-g(x)的两个零点x1∈(1,2),x2∈(9,10),
因此整数a=1,b=9.
点评:本题考查函数的图象与解析式,考查函数的零点,正确运用零点存在定理是关键.

练习册系列答案
相关题目
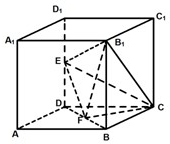 (2012•虹口区三模)如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E、F分别为DD1、DB的中点.
(2012•虹口区三模)如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E、F分别为DD1、DB的中点.