题目内容
利用导数求和:(1)Sn=1+2x+3x2+…+nxn-1(x≠0,n∈N*);
(2)Sn=Cn1+2Cn2+3Cn3+…+nCnn(n∈N*).
【答案】分析:(1)当x=1时,Sn易求;当x≠1时,对x+x2+x3++xn=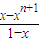 两边求导数可得答案.
两边求导数可得答案.
(2)对(1+x)n=1+Cn1x+Cn2x2++Cnnxn两边求导数后令x=1可得答案.
解答:解:(1)当x=1时,Sn=1+2+3+…+n=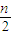 (n+1),
(n+1),
当x≠1时,∵x+x2+x3++xn=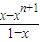 ,
,
两边对x求导,得Sn=1+2x+3x2+…+nxn-1=( )′=
)′=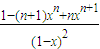 .
.
(2)∵(1+x)n=1+Cn1x+Cn2x2+…+Cnnxn,
两边对x求导,得n(1+x)n-1=Cn1+2Cn2x+3Cn3x2+…+nCnnxn-1.
令x=1,得n•2n-1=Cn1+2Cn2+3Cn3+…+nCnn,
即Sn=Cn1+2Cn2+3Cn3++nCnn=n•2n-1.
点评:本题主要考查导数的运算性质,属中档题.
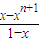 两边求导数可得答案.
两边求导数可得答案.(2)对(1+x)n=1+Cn1x+Cn2x2++Cnnxn两边求导数后令x=1可得答案.
解答:解:(1)当x=1时,Sn=1+2+3+…+n=
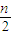 (n+1),
(n+1),当x≠1时,∵x+x2+x3++xn=
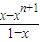 ,
,两边对x求导,得Sn=1+2x+3x2+…+nxn-1=(
 )′=
)′=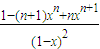 .
.(2)∵(1+x)n=1+Cn1x+Cn2x2+…+Cnnxn,
两边对x求导,得n(1+x)n-1=Cn1+2Cn2x+3Cn3x2+…+nCnnxn-1.
令x=1,得n•2n-1=Cn1+2Cn2+3Cn3+…+nCnn,
即Sn=Cn1+2Cn2+3Cn3++nCnn=n•2n-1.
点评:本题主要考查导数的运算性质,属中档题.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目