题目内容
椭圆为封闭图形,双曲线、抛物线为不封闭图形,其图形不一样,但它们都可以用平面截对顶圆锥面得到,它们都满足曲线上的点到焦点的距离与到准线的距离之比为常数,即离心率e,定义上的统一,必然也蕴含着图形统一,应该如何解释这种现象呢?
思路:三条圆锥曲线都为封闭图形,其形状都为椭圆,所以,圆锥曲线在图形上依然存在着统一.探究:我们知道,椭圆时离心率e越大,椭圆越扁;双曲线时离心率e越大,双曲线开口越大.随着e的增大,椭圆越变越扁,但左半部分开口越来越大,左顶点离l越来越近,而右顶点离F点越来越远;当e趋近于1时,左顶点趋近于F与l间的中点,而右顶点趋向无穷远处;当e=1时,我们可以大胆地认为右顶点在无穷远处,此时曲线变为抛物线;当e>1时,开口越来越大,右顶点超过无穷远处并开始返回,此时曲线变为双曲线两支,或认为双曲线两支无限延伸交于无穷远处,如图3-3-3.
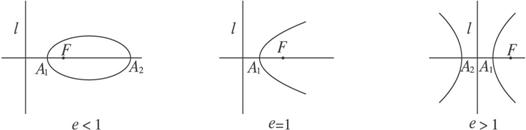
图3-3-3
于是我们可以猜想:三条圆锥曲线都为封闭图形,其形状都为椭圆,所以,圆锥曲线在图形上依然存在着统一,这是一种无限的思想.
因为顶点(曲线与两个坐标轴的交点)如A1是圆锥曲线上的点,所以满足![]() =e,当e→1时,A1向中点靠近;当e=1时,A1位于中点;当e→+∞时,A1向N靠近.这里A1只是
=e,当e→1时,A1向中点靠近;当e=1时,A1位于中点;当e→+∞时,A1向N靠近.这里A1只是![]() 的内分点,其实满足
的内分点,其实满足![]() =e还有一个外分点,即另一顶点A2,满足
=e还有一个外分点,即另一顶点A2,满足![]() =-e.当e<1时,圆锥曲线为椭圆,所以它的外分点A2位于NF的延长线上;当e→1时,A2离F点越远;当e=1时,外分点不存在,或者我们就可以理解为A2位于无穷远处,所以抛物线只有一个顶点;当e>1时,圆锥曲线为双曲线,外分点A2位于NF的反向延长线上;e→+∞时,A2从左侧向N靠近.
=-e.当e<1时,圆锥曲线为椭圆,所以它的外分点A2位于NF的延长线上;当e→1时,A2离F点越远;当e=1时,外分点不存在,或者我们就可以理解为A2位于无穷远处,所以抛物线只有一个顶点;当e>1时,圆锥曲线为双曲线,外分点A2位于NF的反向延长线上;e→+∞时,A2从左侧向N靠近.
这也揭示了为什么椭圆有两个顶点,抛物线只有一个顶点,双曲线有两个顶点,及它们之间的区别,你可以由此进一步理解圆锥曲线的内在统一性.

练习册系列答案
相关题目
 ,那么甲的面积是乙的面积的
,那么甲的面积是乙的面积的 、乙:小矩形
、乙:小矩形 )、②(甲:大直角三角形
)、②(甲:大直角三角形 乙:小直角三角形
乙:小直角三角形 )中体会这个原理,现在图③中的曲线分别是
)中体会这个原理,现在图③中的曲线分别是 与
与 ,运用上面的原理,图③中椭圆的面积为
.
,运用上面的原理,图③中椭圆的面积为
.