题目内容
等比数列{an}的各项均为正数,2a4,a3,4a5成等差数列,且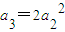 .
.(1)求数列{an}的通项公式;
(2)设
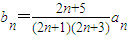 ,求数列{bn}的前n项和Sn.
,求数列{bn}的前n项和Sn.
【答案】分析:(1)设等比数列{an}的公比为q,然后将条件都转化成首项和公比,解方程可求出首项和公比,从而可求出数列{an}的通项公式;
(2)先求出数列{bn}的通项公式,然后利用裂项求和可求出数列{bn}的前n项和Sn.
解答:(本小题满分14分)
(1)解:设等比数列{an}的公比为q,依题意,有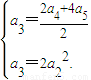 即
即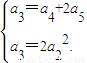 …(2分)
…(2分)
所以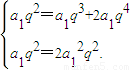 …(3分)
…(3分)
由于a1≠0,q≠0,解之得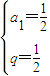 或
或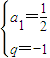 …(5分)
…(5分)
又a1>0,q>0,所以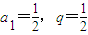 ,…(6分)
,…(6分)
所以数列{an}的通项公式为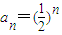 (n∈N*).…(7分)
(n∈N*).…(7分)
(2)解:由(1),得 =
=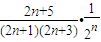 .…(8分)
.…(8分)
所以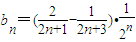 =
=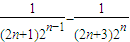 .…(10分)
.…(10分)
所以Sn=b1+b2+…+bn=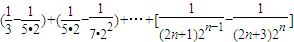 =
=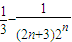 .
.
故数列{bn}的前n项和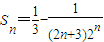 .…(14分)
.…(14分)
点评:本小题主要考查等比数列的通项、裂项求和等知识,考查化归与转化的数学思想方法,以及抽象概括能力、运算求解能力和创新意识,属于中档题.
(2)先求出数列{bn}的通项公式,然后利用裂项求和可求出数列{bn}的前n项和Sn.
解答:(本小题满分14分)
(1)解:设等比数列{an}的公比为q,依题意,有
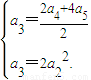 即
即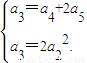 …(2分)
…(2分)所以
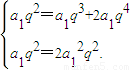 …(3分)
…(3分)由于a1≠0,q≠0,解之得
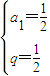 或
或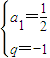 …(5分)
…(5分)又a1>0,q>0,所以
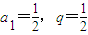 ,…(6分)
,…(6分)所以数列{an}的通项公式为
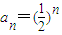 (n∈N*).…(7分)
(n∈N*).…(7分)(2)解:由(1),得
 =
=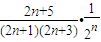 .…(8分)
.…(8分)所以
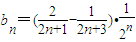 =
=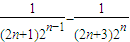 .…(10分)
.…(10分)所以Sn=b1+b2+…+bn=
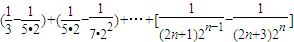 =
=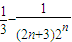 .
.故数列{bn}的前n项和
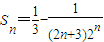 .…(14分)
.…(14分)点评:本小题主要考查等比数列的通项、裂项求和等知识,考查化归与转化的数学思想方法,以及抽象概括能力、运算求解能力和创新意识,属于中档题.

练习册系列答案
相关题目
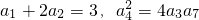 ,则数列{an}的通项公式为________.
,则数列{an}的通项公式为________. ,则数列{an}的通项公式为 .
,则数列{an}的通项公式为 .