Question

（2012•贵州模拟）设函数f（x）=|x+2|-|x-1|
（I）画出函数y=f（x）的图象；
（II）若关于x的不等式f（x）+4≥|1-2m|有解，求实数m的取值范围．

Answer 1

分析：（I）先将原函数式可化为一个分段函数的形式，再分段画出函数在各段上的图象即得原函数的图象．
（II）关于x的不等式f（x）+4≥|1-2m|有解等价于：（f（x）+4）_max≥|1-2m|，再根据分段函数的图象，确定函数的最大值，从而可求实数m的取值范围．

解答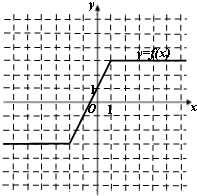：解：（I）函数f（x）可化为：…3′
其图象如下：…5′
（II）关于x的不等式f（x）+4≥|1-2m|有解等价于：
（f（x）+4）_max≥|1-2m|．…6′
由（I）可知f（x）_max=3，
（也可由|f（x）|=||x+2|-|x-1||≤|（x+2）-（x-1|）|=3，得f（x）_max=3）…8′
于是|1-2m|≤7，
解得实数m的取值范围：m∈[-3，4]…10′

点评：本题考查绝对值函数，考查分类讨论、数形结合的数学思想，利用绝对值的几何意义正确分类是关键．