题目内容
15、设函数f(x)的图象与直线x=a,x=b及x轴所围成图形的面积称为函数f(x)在[a,b]上的面积,已知函数y=sinnx在[0,
15.![]() ,
,![]()
(1)
解析:令n=3,则y=sin3x在[0, ![]() ]上的面积为
]上的面积为![]() .
.
又∵y=sin3x在[0, ![]() ]和[
]和[![]() ,
,![]() ]上的面积相等,
]上的面积相等,
所以y=sin3x在[0, ![]() ]上的面积为2·
]上的面积为2·![]() =
=![]() .
.
(2)
解析:由y=sin(3x-π)+1,
设3![]() =3x-π,∴y=sin3
=3x-π,∴y=sin3![]() +1.
+1.
又∵x∈[![]() ,
,![]() ],∴3
],∴3![]() ∈[0,3π],∴
∈[0,3π],∴![]() ∈[0,π].
∈[0,π].
由(1)y=sin3![]() 在[0,
在[0, ![]() ]上的面积为
]上的面积为![]() ,y=sin3
,y=sin3![]() 在[0,π]上的面积为S1+S2+S3-S4=2×
在[0,π]上的面积为S1+S2+S3-S4=2×![]() -
-![]() +S3=
+S3=![]() +S3,
+S3,
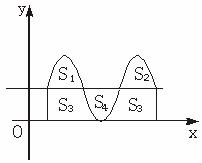
∴S3=1×(![]() -
-![]() )=π,
)=π,
∴y=sin(3x-π)+1在[![]() ,
,![]() ]上的面积为π+
]上的面积为π+![]() .
.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目



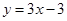 , 求
, 求 的值;
的值; , 求函数
, 求函数 的单调区间.
的单调区间.