题目内容
(本题14分)已知函数, 
(Ⅰ) 设函数f(x)的图象与x轴交点为A, 曲线y=f(x)在A点处的切线方程是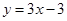 , 求
, 求 的值;
的值;
(Ⅱ) 若函数 , 求函数
, 求函数 的单调区间.
的单调区间.
(Ⅰ)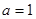 ,
,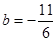 .
.
(Ⅱ)当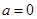 时,
时,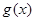 的单调递增区间为
的单调递增区间为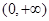 ,单调递减区间为
,单调递减区间为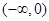 ;
;
当 时,
时,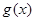 的单调递增区间为
的单调递增区间为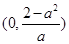 ,单调递减区间为
,单调递减区间为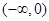 和
和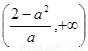 ,
,
当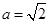 时,
时,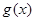 的单调递减区间为
的单调递减区间为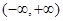 ;
;
当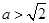 时,
时,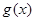 的单调递增区间为
的单调递增区间为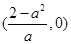 ,单调递减区间为
,单调递减区间为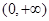 ,
, .
.
当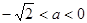 时,
时,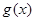 的单调递减区间为
的单调递减区间为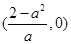 ,单调递增区间为
,单调递增区间为 和
和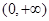 ,
,
当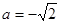 时,
时,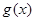 的单调递增区间为
的单调递增区间为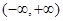 ;
;
当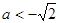 时,
时,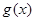 的单调递增区间为
的单调递增区间为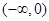 和
和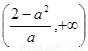 ,单调递减区间为
,单调递减区间为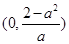 .
.
【解析】本试题主要是考查了导数在研究函数中的运用。利用导数的几何意义求解切线方程,利用导数求解函数的单调区间的综合运用。
(1)根据已知条件,可知∵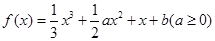 ,∴
,∴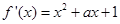
∵ 在
在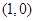 处切线方程为
处切线方程为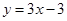 ,
,
∴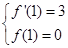 ∴
∴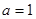 ,
,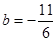 ,求解得到。
,求解得到。
(2)对于参数a分情况讨论。判定导数的符号,确定函数的单调性即可。
解:(Ⅰ)∵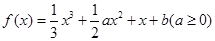 ,
,
∴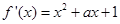 .
……1分
.
……1分
∵ 在
在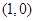 处切线方程为
处切线方程为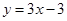 ,
,
∴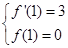 ,
……3分
,
……3分
∴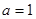 ,
,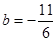 .
(各1分)
……5分
.
(各1分)
……5分
(Ⅱ)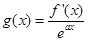
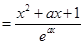
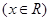 .
.

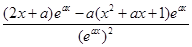
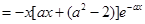 . ……7分
. ……7分
①当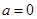 时,
时,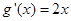 ,
,
|
|
|
0 |
|
|
|
- |
0 |
+ |
|
|
|
极小值 |
|
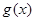 的单调递增区间为
的单调递增区间为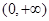 ,单调递减区间为
,单调递减区间为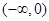 . …9分
. …9分
②当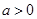 时,令
时,令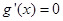 ,得
,得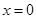 或
或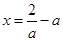 ……10分
……10分
(ⅰ)当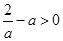 ,即
,即 时,
时,
|
|
|
0 |
|
|
|
|
|
- |
0 |
+ |
0 |
- |
|
|
|
极小值 |
|
极大值 |
|
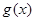 的单调递增区间为
的单调递增区间为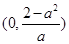 ,单调递减区间为
,单调递减区间为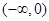 ,
,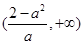 ;---11分
;---11分
(ⅱ)当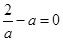 ,即
,即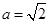 时,
时,
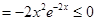 ,
,
故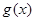 在
在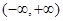 单调递减;
……12分
单调递减;
……12分
(ⅲ)当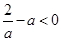 ,即
,即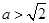 时,
时,
|
|
|
|
|
0 |
|
|
|
- |
0 |
+ |
0 |
- |
|
|
|
极小值 |
|
极大值 |
|
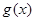 在
在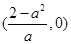 上单调递增,在
上单调递增,在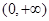 ,
, 上单调递 …13分
上单调递 …13分
综上所述,当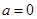 时,
时,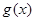 的单调递增区间为
的单调递增区间为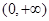 ,单调递减区间为
,单调递减区间为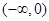 ;
;
当 时,
时,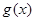 的单调递增区间为
的单调递增区间为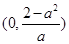 ,单调递减区间为
,单调递减区间为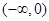 和
和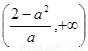 ,
,
当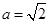 时,
时,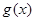 的单调递减区间为
的单调递减区间为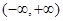 ;
;
当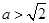 时,
时,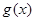 的单调递增区间为
的单调递增区间为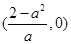 ,单调递减区间为
,单调递减区间为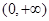 ,
, .
.
当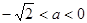 时,
时,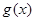 的单调递减区间为
的单调递减区间为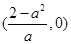 ,单调递增区间为
,单调递增区间为 和
和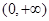 ,
,
当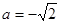 时,
时,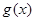 的单调递增区间为
的单调递增区间为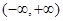 ;
;
当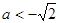 时,
时,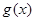 的单调递增区间为
的单调递增区间为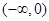 和
和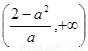 ,单调递减区间为
,单调递减区间为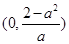

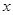
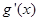

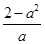
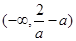


 ,如果满足;对任意
,如果满足;对任意 ,存在常数
,存在常数 ,都有
,都有 成立,则称
成立,则称 ,
,
 时,求函数
时,求函数 上的值域,并判断函数
上的值域,并判断函数 上是以3为上界函数值,求实数
上是以3为上界函数值,求实数 的取值范围;
的取值范围; ,求函数
,求函数 在
在 上的上界T的取值范围。
上的上界T的取值范围。 ,如果满足;对任意
,如果满足;对任意 ,存在常数
,存在常数 ,都有
,都有 成立,则称
成立,则称 ,
,
 时,求函数
时,求函数 上的值域,并判断函数
上的值域,并判断函数 上是以3为上界函数值,求实数
上是以3为上界函数值,求实数 的取值范围;
的取值范围; ,求函数
,求函数 在
在 上的上界T的取值范围。
上的上界T的取值范围。