题目内容
在△ABC中,A、B、C是三角形的三内角, 是三内角对应的三边,已知
是三内角对应的三边,已知 .(1)求角A的大小;(2)若
.(1)求角A的大小;(2)若 =
=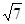 ,且△ABC的面积为
,且△ABC的面积为 ,求
,求 的值.
的值.
(1) ;(2)5.
;(2)5.
解析试题分析:(1)利用余弦定理表示出cosA,将已知等式代入计算求出cosA的值,由A为三角形的内角,利用特殊角的三角函数值即可求出A的度数;
(2)利用三角形的面积公式列出关系式,将a,sinA及已知面积代入求出bc的值,再利用余弦定理列出关系式,将bc的值代入求出b2+c2的值,进而求出b+c的值.
(1) ,又
,又 为三角形内角,所以
为三角形内角,所以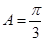 ;
;
(2) ,
,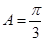
 由面积公式得
由面积公式得  ,即
,即 ①由余弦定理得
①由余弦定理得 ,即
,即 ②,由②变形得
②,由②变形得 ,故
,故
考点:余弦定理;正弦定理的应用.

练习册系列答案
 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
 分别是
分别是 中角
中角 的对边,且
的对边,且 ,
, 的大小;⑵若
的大小;⑵若 ,求
,求 的值.
的值.
 分别为角A、B、C所对的边,已知
分别为角A、B、C所对的边,已知 ,
, 的值;
的值; 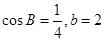 ,求△ABC的面积.
,求△ABC的面积.
 、
、 是两个小区所在地,
是两个小区所在地, 的垂直距离分别为
的垂直距离分别为
 ,
,
 ,在
,在 、
、 、
、 ,在
,在 处建造一个垃圾处理厂,使得
处建造一个垃圾处理厂,使得

 ,且
,且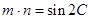 .
. ,求边c的长.
,求边c的长. .
. ,且
,且 ,求
,求 的值;
的值; ,且△ABC的面积为
,且△ABC的面积为 ,求sinA+sinB的值.
,求sinA+sinB的值. ,sinB=
,sinB= cosC.
cosC. ,求△ABC的面积.
,求△ABC的面积.