题目内容
已知函数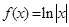
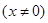 ,函数
,函数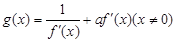
①当 时,求函数
时,求函数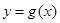 的表达式;
的表达式;
②若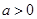 ,函数
,函数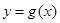 在
在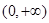 上的最小值是2 ,求
上的最小值是2 ,求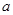 的值;
的值;
③在②的条件下,求直线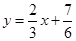 与函数
与函数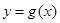 的图象所围成图形的面积.
的图象所围成图形的面积.
【答案】
⑴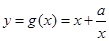 .⑵
.⑵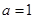 .⑶
.⑶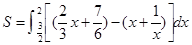 =
=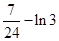 .
.
【解析】
试题分析:⑴∵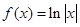 ,
,
∴当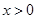 时,
时,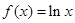 ; 当
; 当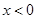 时,
时,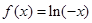
∴当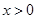 时,
时,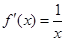 ; 当
; 当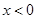 时,
时, .
.
∴当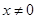 时,函数
时,函数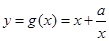 .
.
⑵∵由⑴知当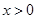 时,
时,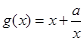 ,
,
∴当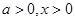 时,
时, 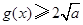 当且仅当
当且仅当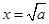 时取等号.
时取等号.
∴函数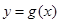 在
在 上的最小值是
上的最小值是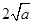 ,∴依题意得
,∴依题意得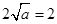 ∴
∴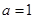 .
.
⑶由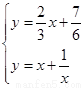 解得
解得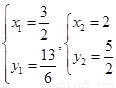
∴直线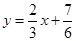 与函数
与函数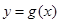 的图象所围成图形的面积
的图象所围成图形的面积
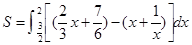 =
=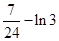 .
.
考点:本题主要考查导数计算,应用导数研究函数的单调性、最值,定积分计算。
点评:典型题,在给定区间,导数值非负,函数是增函数,导数值为非正,函数为减函数。求最值的步骤:计算导数、求驻点、讨论驻点附近导数的正负、确定极值、计算的导函数值比较大小。

练习册系列答案
相关题目

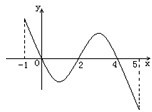 已知函数f(x)的定义域为[-1,5],部分对应值如下表,f(x)的导函数y=f′(x)的图象如图所示.给出关于f(x)的下列命题:
已知函数f(x)的定义域为[-1,5],部分对应值如下表,f(x)的导函数y=f′(x)的图象如图所示.给出关于f(x)的下列命题: