题目内容
设两个非零向量e1和e2不共线.
(1)如果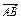 =e1-e2,
=e1-e2,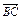 =3e1+2e2,
=3e1+2e2,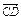 =-8e1-2e2,
=-8e1-2e2,
求证:A、C、D三点共线;
(2)如果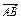 =e1+e2,
=e1+e2,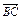 =2e1-3e2,
=2e1-3e2,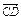 =2e1-ke2,且A、C、D三点共线,求k的值.
=2e1-ke2,且A、C、D三点共线,求k的值.
(1)如果
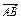 =e1-e2,
=e1-e2,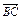 =3e1+2e2,
=3e1+2e2,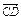 =-8e1-2e2,
=-8e1-2e2,求证:A、C、D三点共线;
(2)如果
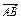 =e1+e2,
=e1+e2,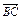 =2e1-3e2,
=2e1-3e2,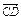 =2e1-ke2,且A、C、D三点共线,求k的值.
=2e1-ke2,且A、C、D三点共线,求k的值.(1)证明见解析(2)k=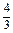
(1)证明 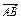 =e1-e2,
=e1-e2,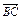 =3e1+2e2,
=3e1+2e2, 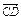 =-8e1-2e2,
=-8e1-2e2,
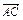 =
=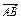 +
+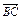 =4e1+e2
=4e1+e2
=-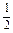 (-8e1-2e2)=-
(-8e1-2e2)=-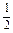
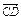 ,
,
∴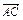 与
与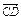 共线,
共线,
又∵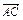 与
与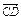 有公共点C,
有公共点C,
∴A、C、D三点共线.
(2)解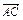 =
=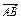 +
+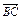 =(e1+e2)+(2e1-3e2)=3e1-2e2,
=(e1+e2)+(2e1-3e2)=3e1-2e2,
∵A、C、D三点共线,
∴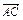 与
与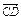 共线,从而存在实数
共线,从而存在实数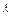 使得
使得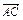 =
=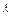
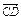 ,
,
即3e1-2e2=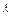 (2e1-ke2),由平面向量的基本定理,
(2e1-ke2),由平面向量的基本定理,
得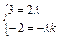 ,解之得
,解之得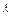 =
=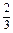 ,k=
,k=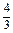 .
.
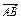 =e1-e2,
=e1-e2,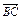 =3e1+2e2,
=3e1+2e2, 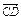 =-8e1-2e2,
=-8e1-2e2,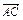 =
=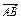 +
+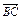 =4e1+e2
=4e1+e2=-
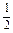 (-8e1-2e2)=-
(-8e1-2e2)=-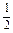
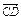 ,
,∴
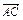 与
与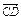 共线,
共线,又∵
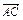 与
与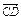 有公共点C,
有公共点C,∴A、C、D三点共线.
(2)解
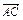 =
=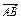 +
+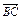 =(e1+e2)+(2e1-3e2)=3e1-2e2,
=(e1+e2)+(2e1-3e2)=3e1-2e2,∵A、C、D三点共线,
∴
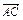 与
与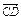 共线,从而存在实数
共线,从而存在实数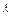 使得
使得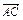 =
=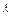
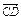 ,
,即3e1-2e2=
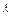 (2e1-ke2),由平面向量的基本定理,
(2e1-ke2),由平面向量的基本定理,得
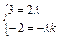 ,解之得
,解之得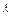 =
=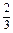 ,k=
,k=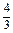 .
.
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
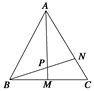
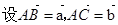 ,点N在AC上,且AN=2NC,AM与BN相交于点P,AP=λAM,求(1)λ的值 (2)
,点N在AC上,且AN=2NC,AM与BN相交于点P,AP=λAM,求(1)λ的值 (2)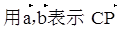

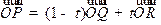 .
.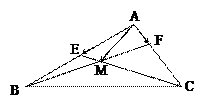
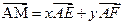 ,则
,则 
 ( )
( )



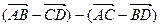
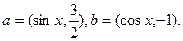
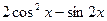 的值;
的值;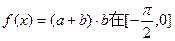 上的最大值
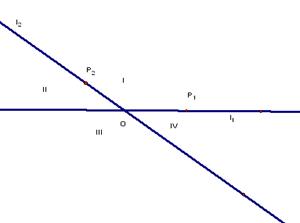
上的最大值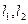 将平面分割成
将平面分割成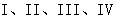 四个区域(不包含边界),向量
四个区域(不包含边界),向量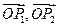 分别为
分别为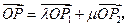 且点P落在第
且点P落在第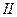 区域,则实数
区域,则实数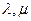 满足
满足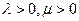
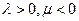
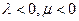
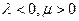
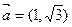 ,
,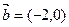 ,则
,则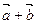 =_____________________.
=_____________________.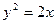 与过焦点的直线交于A,B两点,则
与过焦点的直线交于A,B两点,则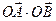 的值为________
的值为________