题目内容
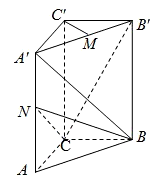 如图所示,直三棱柱ABC-A'B'C'中,∠BCA=90°,CA=CB=1,AA'=2,M,N分别是A'B'、A'A的中点.
如图所示,直三棱柱ABC-A'B'C'中,∠BCA=90°,CA=CB=1,AA'=2,M,N分别是A'B'、A'A的中点.
(1)求证:A'B⊥C'M;
(2)求异面直线BA'与CB'所成交的大小;
(3)(理)求BN与平面CNB'所称的角的大小;
(4)(理)求二面角A-BN-C的大小.
解:(1)以C为坐标原点,CB,CA,CC′分别为x轴,y轴,z轴,则B(1,0,0),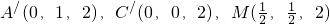
∴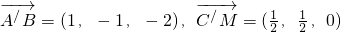
∴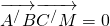
∴A'B⊥C'M;
(2)∵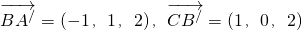
∴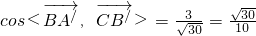
∴异面直线BA'与CB'所成角为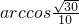 ;
;
(3)设BN与平面CNB'所成的角为α,平面CNB'的一个法向量为(x,y,z)
∵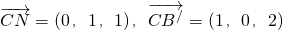
∴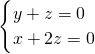
∴平面CNB'的一个法向量为(2,1,-1)
∵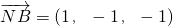
∴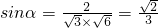
∴BN与平面CNB'所成的角为 ;
;
(4)设平面NBC的一个法向量为(a,b,c ),二面角A-BN-C的大小为β
∵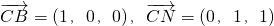
∴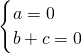
∴平面NBC的一个法向量为(0,1,-1)
∵平面ABN的一个法向量为(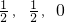 )
)
∴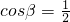 ,∴β=60°
,∴β=60°
∴二面角A-BN-C的大小为60°
分析:以C为坐标原点,CB,CA,CC′分别为x轴,y轴,z轴建立空间直角坐标系,用坐标表示向量,从而可证线线垂直,可求线线角,线面角,二面角,注意法向量的求解方法.
点评:本题的考点是与二面角有关的立体几何综合问题,主要考查线线垂直,线面角、二面角等,关键是建立空间直角坐标系,利用向量的方法求解.
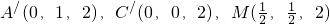
∴
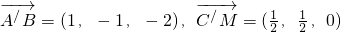
∴
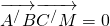
∴A'B⊥C'M;
(2)∵
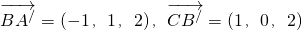
∴
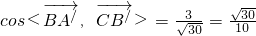
∴异面直线BA'与CB'所成角为
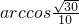 ;
;(3)设BN与平面CNB'所成的角为α,平面CNB'的一个法向量为(x,y,z)
∵
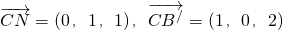
∴
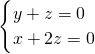
∴平面CNB'的一个法向量为(2,1,-1)
∵
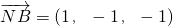
∴
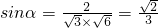
∴BN与平面CNB'所成的角为
 ;
;(4)设平面NBC的一个法向量为(a,b,c ),二面角A-BN-C的大小为β
∵
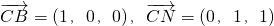
∴
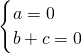
∴平面NBC的一个法向量为(0,1,-1)
∵平面ABN的一个法向量为(
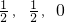 )
)∴
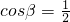 ,∴β=60°
,∴β=60°∴二面角A-BN-C的大小为60°
分析:以C为坐标原点,CB,CA,CC′分别为x轴,y轴,z轴建立空间直角坐标系,用坐标表示向量,从而可证线线垂直,可求线线角,线面角,二面角,注意法向量的求解方法.
点评:本题的考点是与二面角有关的立体几何综合问题,主要考查线线垂直,线面角、二面角等,关键是建立空间直角坐标系,利用向量的方法求解.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案
相关题目
 如图所示,直三棱柱ABC-A1B1C1的各条棱长均为a,D是侧棱CC1的中点.
如图所示,直三棱柱ABC-A1B1C1的各条棱长均为a,D是侧棱CC1的中点. 如图所示,直三棱柱ABC-A1B1C1中,AB⊥AC,D,E分别为AA1,B1C的中点,若记
如图所示,直三棱柱ABC-A1B1C1中,AB⊥AC,D,E分别为AA1,B1C的中点,若记 如图所示,直三棱柱ABC-A'B'C'中,∠BCA=90°,CA=CB=1,AA'=2,M,N分别是A'B'、A'A的中点.
如图所示,直三棱柱ABC-A'B'C'中,∠BCA=90°,CA=CB=1,AA'=2,M,N分别是A'B'、A'A的中点.
