Question

如图所示,在直三棱柱ABC—A₁B₁C₁中,∠ABC=90°,D为棱AC的中点,且AB=BC=BB₁=a.

(1)求证:AB₁∥平面BC₁D;

(2)求异面直线AB₁与BC₁所成的角;

(3)求点A到平面BC₁D的距离.

Answer 1

(1)证明:连结B₁C交BC₁于E,连结ED.?

∵B₁BCC₁是矩形且D为棱AC的中点,∴AB₁∥ED.?

又AB₁平面BC₁D,ED平面BC₁D,∴AB₁∥平面BC₁D.?

(2)解析:由(1)知∠DEB是异面直线AB₁与BC₁所成的角,?

∵AB=BC=BB₁=a,?

∴AC=a,BD=a,BE=a,AB₁=a.??

∵AB₁∥ED,且D为棱AC的中点,?

∴DE=AB₁=a.?

在△BDE中,BD=BE=DE,?

∴∠DEB=60°.?

∴异面直线AB₁与BC₁所成的角为60°.?

(3)解析:∵D为棱AC的中点,∴点A到平面BC₁D的距离与点C到平面BC₁D的距离相等.?

设点C到平面BC₁D的距离为h,?

∵V_C—BC1D?=V_C1—BCD?,?

∴S_△BC1D?·h=S_△BCD?·CC₁.?

∴h=.?

∵BD=a,BC₁=a,C₁D=a,?

∴BD²+C₁D²=2a²=BC₁².?

∴∠BDC₁=90°.?

∴S_△BC1D?=BD·C₁D=·a·a=a².?

又S_△BCD?=BD·CD=·a·a =a² ,CC₁=a,?

∴h=.?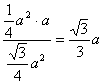

∴点A到平面BC₁D的距离为a.