题目内容
(本小题满分12分)设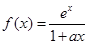 ,其中
,其中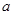 为正实数
为正实数
(1)当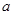
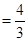 时,求
时,求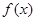 的极值点;
的极值点;
(2)若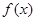 为
为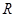 上的单调函数,求
上的单调函数,求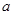 的取值范围。
的取值范围。
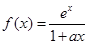 ,其中
,其中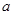 为正实数
为正实数(1)当
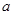
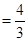 时,求
时,求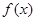 的极值点;
的极值点;(2)若
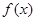 为
为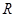 上的单调函数,求
上的单调函数,求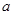 的取值范围。
的取值范围。对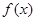 求导得
求导得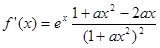
(1)当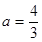 时,若
时,若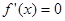 ,则
,则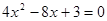 ,解得
,解得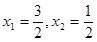 ,结合①,可得
,结合①,可得
所以,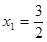 是极小值点,
是极小值点,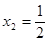 是极
是极 大值点.
大值点.
(2)若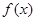 为R上的单调函数,则
为R上的单调函数,则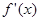 在R上不变号,结合①与条件
在R上不变号,结合①与条件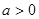 ,知在R上恒成立,因此
,知在R上恒成立,因此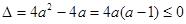 ,由此并结合
,由此并结合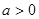
 ,知
,知 .
.
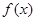 求导得
求导得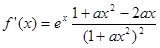
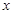 | 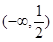 | 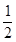 | 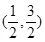 | 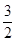 | 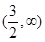 |
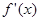 | + | 0 | - | 0 | + |
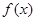 |  | 极大值 | | 极小值 | |
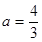 时,若
时,若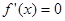 ,则
,则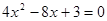 ,解得
,解得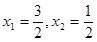 ,结合①,可得
,结合①,可得所以,
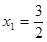 是极小值点,
是极小值点,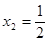 是极
是极 大值点.
大值点.(2)若
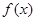 为R上的单调函数,则
为R上的单调函数,则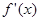 在R上不变号,结合①与条件
在R上不变号,结合①与条件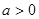 ,知在R上恒成立,因此
,知在R上恒成立,因此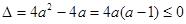 ,由此并结合
,由此并结合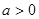
 ,知
,知 .
.略

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
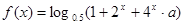 ;
;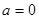 ,求
,求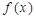 的值域;(2)在(1)的条件下,判断
的值域;(2)在(1)的条件下,判断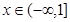 时
时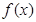 有意义求实
有意义求实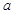 的范围。
的范围。 定义域中任意的x1,x2(x1≠x2)有如下结论:
定义域中任意的x1,x2(x1≠x2)有如下结论: ②
②
 ④
④
 时,上述结论中正确的是( )
时,上述结论中正确的是( ) 的值为
的值为 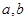 ,可按规则
,可按规则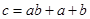 扩充为一个新数
扩充为一个新数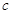 ,在
,在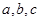 三个数中取两个较大的数,按上述规则扩充得到一个新数,依次下去,将每扩充一次得到一个新数称为一次操作.
三个数中取两个较大的数,按上述规则扩充得到一个新数,依次下去,将每扩充一次得到一个新数称为一次操作.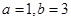 ,按上述规则操作三次,扩充所得的数是__________;
,按上述规则操作三次,扩充所得的数是__________;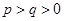 ,经过6次操作后扩充所得的数为
,经过6次操作后扩充所得的数为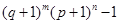 (
(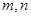 为正整数),则
为正整数),则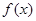 是定义在
是定义在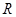 上的偶函数,且
上的偶函数,且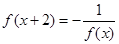 ,若当
,若当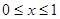 时,
时,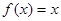 ,则
,则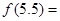 .
.  ,则满足
,则满足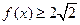 的
的 取值范围为__ ▲ ___
取值范围为__ ▲ ___ |在
|在 [
[ ,1]上增函数,则实数a的取值范围是_____
,1]上增函数,则实数a的取值范围是_____