题目内容
(本小题满分12分)
已知向量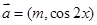 ,
,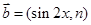 ,设函数
,设函数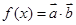 ,且
,且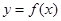 的图象过点
的图象过点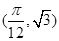 和点
和点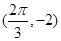 .
.
(Ⅰ)求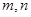 的值;
的值;
(Ⅱ)将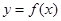 的图象向左平移
的图象向左平移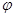 (
(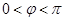 )个单位后得到函数
)个单位后得到函数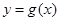 的图象.若
的图象.若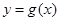 的图象上各最高点到点
的图象上各最高点到点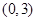 的距离的最小值为1,求
的距离的最小值为1,求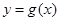 的单调增区间.
的单调增区间.
已知向量
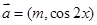 ,
,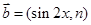 ,设函数
,设函数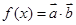 ,且
,且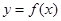 的图象过点
的图象过点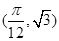 和点
和点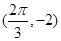 .
.(Ⅰ)求
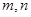 的值;
的值;(Ⅱ)将
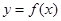 的图象向左平移
的图象向左平移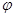 (
(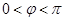 )个单位后得到函数
)个单位后得到函数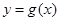 的图象.若
的图象.若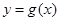 的图象上各最高点到点
的图象上各最高点到点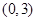 的距离的最小值为1,求
的距离的最小值为1,求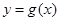 的单调增区间.
的单调增区间.(I)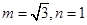 .
.
(II)函数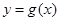 的单调递增区间为
的单调递增区间为 .
.
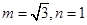 .
.(II)函数
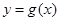 的单调递增区间为
的单调递增区间为 .
.试题分析:(1)由题意知
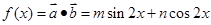 .
.根据
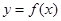 的图象过点
的图象过点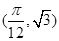 和
和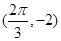 ,得到
,得到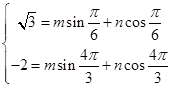 ,
,解得
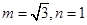 .
.(2)由(1)知:
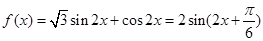 .
.由题意知:
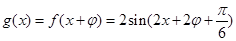 ,
,依题意知到点
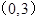 的距离为1的最高点为
的距离为1的最高点为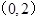 .
.将其代入
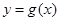 得
得 ,
,可得
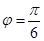 ,得到
,得到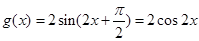 ,
,由
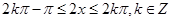 ,得
,得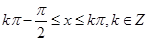 ,
,得到
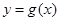 的单调递增区间为
的单调递增区间为 .
.试题解析:(1)由题意知:
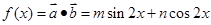 .
.因为
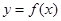 的图象过点
的图象过点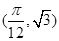 和
和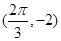 ,
,所以
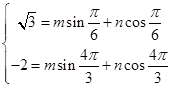 ,
,即
 ,
,解得
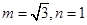 .
.(2)由(1)知:
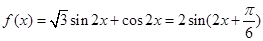 .
.由题意知:
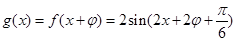 ,
,设
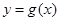 的图象上符合题意的最高点为
的图象上符合题意的最高点为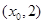 ,
,由题意知:
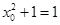 ,所以
,所以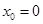 ,
,即到点
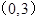 的距离为1的最高点为
的距离为1的最高点为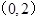 .
.将其代入
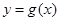 得
得 ,
,因为
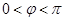 ,所以
,所以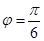 ,
,因此
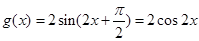 ,
,由
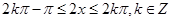 ,得
,得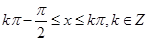 ,
,所以,函数
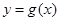 的单调递增区间为
的单调递增区间为 .
.
练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
 (米)是时间
(米)是时间 (
( ,单位:小时,
,单位:小时, 表示0:00—零时)的函数,其函数关系式为
表示0:00—零时)的函数,其函数关系式为

 .已知一天中该港口水位的深度变化有如下规律:出现相邻两次最高水位的深度的时间差为12小时,最高水位的深度为12米,最低水位的深度为6米,每天13:00时港口水位的深度恰为10.5米.
.已知一天中该港口水位的深度变化有如下规律:出现相邻两次最高水位的深度的时间差为12小时,最高水位的深度为12米,最低水位的深度为6米,每天13:00时港口水位的深度恰为10.5米. 的表达式;
的表达式;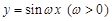 的图象沿x轴方向左平移
的图象沿x轴方向左平移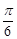 个单位,平移后的图象如右图所示. 则平移后的图象所对应函数的解析式是( )
个单位,平移后的图象如右图所示. 则平移后的图象所对应函数的解析式是( )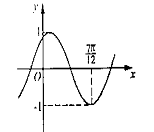




 的图象向左平移
的图象向左平移 个单位,得到函数
个单位,得到函数 的函数图象,则下列说法正确的是( )
的函数图象,则下列说法正确的是( ) 是奇函数
是奇函数
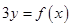 的图像关于直线
的图像关于直线 对称
对称 对称
对称 在曲线
在曲线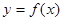 与直线
与直线 的交点中,若相邻交点距离的最小值为
的交点中,若相邻交点距离的最小值为 ,则
,则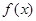 的最小正周期为( )
的最小正周期为( )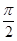



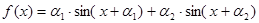 ,其中
,其中 为已知实常数,
为已知实常数, ,则下列命题中错误的是( )
,则下列命题中错误的是( ) ,则
,则 对任意实数
对任意实数 恒成立;
恒成立; ,则函数
,则函数 为奇函数;
为奇函数; ,则函数
,则函数 时,若
时,若 ,则
,则 .
. 的方程
的方程 在区间
在区间 上有两个不同的实数解,则实数
上有两个不同的实数解,则实数 的取值范围为 .
的取值范围为 . 若对任意的
若对任意的 都有
都有 ,则
,则 =__________.
=__________.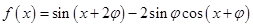 的最大值为_________.
的最大值为_________.