题目内容
【题目】几位同学在研究函数![]()
![]() 时,给出了下面几个结论:
时,给出了下面几个结论:
①![]() 的单调减区间是
的单调减区间是![]() ,单调增区间是
,单调增区间是![]() ;
;
②若![]() ,则一定有
,则一定有![]() ;
;
③函数![]() 的值域为
的值域为![]() ;
;
④若规定![]() ,
,![]() ,则
,则![]() 对任意
对任意![]() 恒成立.
恒成立.
上述结论中正确的是____
【答案】②④
【解析】
根据题意,以此分析命题:①可根据函数的解析式判断出其是一个增函数;②由①可得到结果;③函数f(x)的值域为(﹣1,1),可由绝对值不等式的性质证明得;④由其形式知,此是一个与自然数有关的命题,故采用归纳推理的方法证明,即可得答案.
①函数![]() 是一个奇函数,当x≥0时,
是一个奇函数,当x≥0时,![]() ,判断知函数在(0,+∞)上是一个增函数,由奇函数的性质知,函数
,判断知函数在(0,+∞)上是一个增函数,由奇函数的性质知,函数![]() (x∈R)是一个增函数,故若x1≠x2,则一定有f(x1)≠f(x2),此命题①不正确;
(x∈R)是一个增函数,故若x1≠x2,则一定有f(x1)≠f(x2),此命题①不正确;
②由①已证,故此命题正确;
③|x|<1+|x|,故![]()
![]() ,函数f(x)的值域为(﹣1,1),③不正确;
,函数f(x)的值域为(﹣1,1),③不正确;
④当n=1,f1(x)=f(x)=![]() ,
,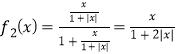 假设n=k时,
假设n=k时,![]() 成立,则n=k+1时,
成立,则n=k+1时,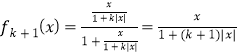 成立,类推可得到,此命题正确.
成立,类推可得到,此命题正确.
故答案为:②④

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目

