题目内容
【题目】如图,⊙O是以AB为直径的圆,点C在圆上,在△ABC和△ACD中,∠ADC=90°,∠BAC=∠CAD,DC的延长线与AB的延长线交于点E.若EB=6,EC=6 ![]() ,则BC的长为 .
,则BC的长为 . 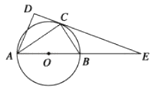
【答案】2 ![]()
【解析】解:连接OC,在直角三角形ACB和ADC中,
∠D=∠ACB,∠CAB=∠DAC,
可得∠DCA=∠CBA,
又OB=OC,即∠CBA=∠BCO,
又∠BCO+∠ACO=90°,
可得∠DCA+∠ACO=90°,
即有OC⊥DE,ED为圆O的切线,
由圆的切割线定理,可得CE2=BEAE,
即有(6 ![]() )2=6(6+AB),
)2=6(6+AB),
解得AB=6,即圆的半径为3,
由AD∥OC,可得 ![]() =
= ![]() ,
,
即为 ![]() =
= ![]() ,即有CD=2
,即有CD=2 ![]() ,
,
又 ![]() =
= ![]() ,即为
,即为 ![]() =
= ![]() ,
,
解得AD=4,AC= ![]() =2
=2 ![]() ,
,
BC= ![]() =
= ![]() =2
=2 ![]() .
.
所以答案是:2 ![]() .
.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目