ĢāÄæÄŚČŻ
£Ø2013•½Ī÷£©ŅŃÖŖŗÆŹżf£Øx£©=a(1-2|x-
|)£¬aĪŖ³£ŹżĒŅa£¾0£®
£Ø1£©f£Øx£©µÄĶ¼Ļó¹ŲÓŚÖ±Ļßx=
¶Ō³Ę£»
£Ø2£©Čōx0Āś×ćf£Øf£Øx0£©£©=x0£¬µ«f£Øx0£©”Łx0£¬Ōņx0³ĘĪŖŗÆŹżf£Øx£©µÄ¶ž½×ÖÜĘŚµć£¬Čē¹ūf£Øx£©ÓŠĮ½øö¶ž½×ÖÜĘŚµćx1£¬x2£¬ŹŌČ·¶ØaµÄȔֵ·¶Ī§£»
£Ø3£©¶ŌÓŚ£Ø2£©ÖŠµÄx1£¬x2£¬ŗĶa£¬Éčx3ĪŖŗÆŹżf£Øf£Øx£©£©µÄ×ī“óÖµµć£¬A£Øx1£¬f£Øf£Øx1£©£©£©£¬B£Øx2£¬f£Øf£Øx2£©£©£©£¬C£Øx3£¬0£©£¬¼Ē”÷ABCµÄĆ껿ĪŖS£Øa£©£¬ĢÖĀŪS£Øa£©µÄµ„µ÷ŠŌ£®
| 1 |
| 2 |
£Ø1£©f£Øx£©µÄĶ¼Ļó¹ŲÓŚÖ±Ļßx=
| 1 |
| 2 |
£Ø2£©Čōx0Āś×ćf£Øf£Øx0£©£©=x0£¬µ«f£Øx0£©”Łx0£¬Ōņx0³ĘĪŖŗÆŹżf£Øx£©µÄ¶ž½×ÖÜĘŚµć£¬Čē¹ūf£Øx£©ÓŠĮ½øö¶ž½×ÖÜĘŚµćx1£¬x2£¬ŹŌČ·¶ØaµÄȔֵ·¶Ī§£»
£Ø3£©¶ŌÓŚ£Ø2£©ÖŠµÄx1£¬x2£¬ŗĶa£¬Éčx3ĪŖŗÆŹżf£Øf£Øx£©£©µÄ×ī“óÖµµć£¬A£Øx1£¬f£Øf£Øx1£©£©£©£¬B£Øx2£¬f£Øf£Øx2£©£©£©£¬C£Øx3£¬0£©£¬¼Ē”÷ABCµÄĆ껿ĪŖS£Øa£©£¬ĢÖĀŪS£Øa£©µÄµ„µ÷ŠŌ£®
·ÖĪö£ŗ£Ø1£©Ö»ŅŖÖ¤Ć÷f(
+x)=f(
-x)³ÉĮ¢¼“æÉ£»
£Ø2£©¶Ōa·ÖĄąĢÖĀŪ£¬ĄūÓƶž½×ÖÜĘŚµćµÄ¶ØŅ弓æÉµĆ³ö£»
£Ø3£©ÓÉ£Ø2£©µĆ³öx3£¬µĆ³öČż½ĒŠĪµÄĆ껿£¬ĄūÓƵ¼Źż¼“æÉµĆ³öĘ䵄µ÷ŠŌ£®
| 1 |
| 2 |
| 1 |
| 2 |
£Ø2£©¶Ōa·ÖĄąĢÖĀŪ£¬ĄūÓƶž½×ÖÜĘŚµćµÄ¶ØŅ弓æÉµĆ³ö£»
£Ø3£©ÓÉ£Ø2£©µĆ³öx3£¬µĆ³öČż½ĒŠĪµÄĆ껿£¬ĄūÓƵ¼Źż¼“æÉµĆ³öĘ䵄µ÷ŠŌ£®
½ā“š£ŗ£Ø1£©Ö¤Ć÷£ŗ”ßf(
+x)=a(1-2|
+x-
|)=a£Ø1-2|x|£©£¬f(
-x)=a(1-2|
-x-
|)=a£Ø1-2|x|£©£¬
”ąf(
+x)=f(
-x)£¬”ąf£Øx£©µÄĶ¼Ļó¹ŲÓŚÖ±Ļßx=
¶Ō³Ę£®
£Ø2£©½ā£ŗµ±0£¼a£¼
Ź±£¬ÓŠf£Øf£Øx£©£©=
£®
”ąf£Øf£Øx£©£©=xÖ»ÓŠŅ»øö½āx=0ÓÖf£Ø0£©=0£¬¹Ź0²»ŹĒ¶ž½×ÖÜĘŚµć£®
µ±a=
Ź±£¬ÓŠf£Øf£Øx£©£©=
£®
”ąf£Øf£Øx£©£©=xÓŠ½ā¼Æ£¬{x|x”Ü
}£¬¹Ź“Ė¼ÆŗĻÖŠµÄĖłÓŠµć¶¼²»ŹĒ¶ž½×ÖÜĘŚµć£®
µ±a£¾
Ź±£¬ÓŠf£Øf£Øx£©£©=
£¬
”ąf£Øf£Øx£©£©=xÓŠĖÄøö½ā£ŗ0£¬
£¬
£¬
£®
ÓÉf£Ø0£©=0£¬f(
)=
£¬f(
)”Ł
£¬f(
)”Ł
£®
¹ŹÖ»ÓŠ
£¬
ŹĒf£Øx£©µÄ¶ž½×ÖÜĘŚµć£¬×ŪÉĻĖłŹö£¬ĖłĒóaµÄȔֵ·¶Ī§ĪŖa£¾
£®
£Ø3£©ÓÉ£Ø2£©µĆx1=
£¬x2=
£®
”ßx2ĪŖŗÆŹżf£Øx£©µÄ×ī“óÖµµć£¬”ąx3=
£¬»ņx3=
£®
µ±x3=
Ź±£¬S£Øa£©=
£®Ēóµ¼µĆ£ŗS”ä£Øa£©=-
£®
”ąµ±a”Ź(
£¬
)Ź±£¬S£Øa£©µ„µ÷µŻŌö£¬µ±a”Ź(
£¬+”Ž)Ź±£¬S£Øa£©µ„µ÷µŻ¼õ£®
µ±x3=
Ź±£¬S£Øa£©=
£¬Ēóµ¼µĆS”ä(a)=
£®
”ßa£¾
£¬“Ó¶ųÓŠS”ä(a)=
£®
”ąµ±a”Ź(
£¬+”Ž)Ź±£¬S£Øa£©µ„µ÷µŻŌö£®
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
”ąf(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
£Ø2£©½ā£ŗµ±0£¼a£¼
| 1 |
| 2 |
|
”ąf£Øf£Øx£©£©=xÖ»ÓŠŅ»øö½āx=0ÓÖf£Ø0£©=0£¬¹Ź0²»ŹĒ¶ž½×ÖÜĘŚµć£®
µ±a=
| 1 |
| 2 |
|
”ąf£Øf£Øx£©£©=xÓŠ½ā¼Æ£¬{x|x”Ü
| 1 |
| 2 |
µ±a£¾
| 1 |
| 2 |
|
”ąf£Øf£Øx£©£©=xÓŠĖÄøö½ā£ŗ0£¬
| 2a |
| 1+4a2 |
| 2a |
| 1+2a |
| 4a2 |
| 1+4a2 |
ÓÉf£Ø0£©=0£¬f(
| 2a |
| 1+2a |
| 2a |
| 1+2a |
| 2a |
| 1+4a2 |
| 2a |
| 1+4a2 |
| 4a2 |
| 1+4a2 |
| 4a2 |
| 1+4a2 |
¹ŹÖ»ÓŠ
| 2a |
| 1+4a2 |
| 4a2 |
| 1+4a2 |
| 1 |
| 2 |
£Ø3£©ÓÉ£Ø2£©µĆx1=
| 2a |
| 1+4a2 |
| 4a2 |
| 1+4a2 |
”ßx2ĪŖŗÆŹżf£Øx£©µÄ×ī“óÖµµć£¬”ąx3=
| 1 |
| 4a |
| 4a-1 |
| 4a |
µ±x3=
| 1 |
| 4a |
| 2a-1 |
| 4(1+4a2) |
2(a-
| ||||||||
| (1+4a2)2 |
”ąµ±a”Ź(
| 1 |
| 2 |
1+
| ||
| 2 |
1+
| ||
| 2 |
µ±x3=
| 4a-1 |
| 4a |
| 8a2-6a+1 |
| 4(1+4a2) |
| 12a2+4a-3 |
| 2(1+4a2)2 |
”ßa£¾
| 1 |
| 2 |
| 12a2+4a-3 |
| 2(1+4a2)2 |
”ąµ±a”Ź(
| 1 |
| 2 |
µćĘĄ£ŗ±¾Ģāæ¼²éĮĖŠĀ¶ØŅå”°¶ž½×ÖÜĘŚµć”±”¢ĄūÓƵ¼ŹżŃŠ¾æŗÆŹżµÄµ„µ÷ŠŌ”¢Čż½ĒŠĪµÄĆ껿µČ»ł“”ÖŖŹ¶£¬æ¼²éĮĖĶĘĄķÄÜĮ¦ŗĶ¼ĘĖćÄÜĮ¦£®

Į·Ļ°²įĻµĮŠ“š°ø
Ļą¹ŲĢāÄæ
 £Ø2013•½Ī÷£©Š”²ØŅŃÓĪĻ··½Ź½¾ö¶ØŹĒČ„“ņĒņ”¢³Ŗøč»¹ŹĒČ„ĻĀĘ壮ÓĪĻ·¹ęŌņĪŖŅŌOĪŖĘšµć£¬ŌŁ“ÓA1£¬A2£¬A3£¬A4£¬A5£¬A6£ØČēĶ¼£©Õā6øöµćÖŠČĪČ”Į½µć·Ö±šĪŖÖÕµćµĆµ½Į½øöĻņĮ棬¼Ē×”ÕāĮ½øöĻņĮæµÄŹżĮæ»żĪŖX£¬ČōX£¾0¾ĶČ„“ņĒņ£¬ČōX=0¾ĶČ„³Ŗøč£¬ČōX£¼0¾ĶČ„ĻĀĘå
£Ø2013•½Ī÷£©Š”²ØŅŃÓĪĻ··½Ź½¾ö¶ØŹĒČ„“ņĒņ”¢³Ŗøč»¹ŹĒČ„ĻĀĘ壮ÓĪĻ·¹ęŌņĪŖŅŌOĪŖĘšµć£¬ŌŁ“ÓA1£¬A2£¬A3£¬A4£¬A5£¬A6£ØČēĶ¼£©Õā6øöµćÖŠČĪČ”Į½µć·Ö±šĪŖÖÕµćµĆµ½Į½øöĻņĮ棬¼Ē×”ÕāĮ½øöĻņĮæµÄŹżĮæ»żĪŖX£¬ČōX£¾0¾ĶČ„“ņĒņ£¬ČōX=0¾ĶČ„³Ŗøč£¬ČōX£¼0¾ĶČ„ĻĀĘå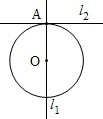 £Ø2013•½Ī÷£©ČēĶ¼£®ŅŃÖŖl1”Ķl2£¬Ō²ŠÄŌŚl1ÉĻ”¢°ė¾¶ĪŖ1mµÄŌ²OŌŚt=0Ź±Óėl2ĻąĒŠÓŚµćA£¬Ō²OŃŲl1ŅŌ1m/sµÄĖŁ¶ČŌČĖŁĻņÉĻŅĘ¶Æ£¬Ō²±»Ö±Ļßl2Ėł½ŲÉĻ·½Ō²»”³¤¼ĒĪŖx£¬Įīy=cosx£¬ŌņyÓėŹ±¼ät£Ø0”Üt”Ü1£¬µ„Ī»£ŗs£©µÄŗÆŹży=f£Øt£©µÄĶ¼Ļó“óÖĀĪŖ£Ø””””£©
£Ø2013•½Ī÷£©ČēĶ¼£®ŅŃÖŖl1”Ķl2£¬Ō²ŠÄŌŚl1ÉĻ”¢°ė¾¶ĪŖ1mµÄŌ²OŌŚt=0Ź±Óėl2ĻąĒŠÓŚµćA£¬Ō²OŃŲl1ŅŌ1m/sµÄĖŁ¶ČŌČĖŁĻņÉĻŅĘ¶Æ£¬Ō²±»Ö±Ļßl2Ėł½ŲÉĻ·½Ō²»”³¤¼ĒĪŖx£¬Įīy=cosx£¬ŌņyÓėŹ±¼ät£Ø0”Üt”Ü1£¬µ„Ī»£ŗs£©µÄŗÆŹży=f£Øt£©µÄĶ¼Ļó“óÖĀĪŖ£Ø””””£©