题目内容
【题目】已知函数f(x)=![]() ,其中a>0且a≠1,若a=
,其中a>0且a≠1,若a=![]() 时方程f(x)=b有两个不同的实根,则实数b的取值范围是______;若f(x)的值域为[3,+∞],则实数a的取值范围是______.
时方程f(x)=b有两个不同的实根,则实数b的取值范围是______;若f(x)的值域为[3,+∞],则实数a的取值范围是______.
【答案】(1)(3,![]() ) (2)[
) (2)[![]() ,1)∪(1,+∞)
,1)∪(1,+∞)
【解析】
(1).作出![]() 的图象,由图象即可得到
的图象,由图象即可得到![]() 和
和![]() 有两个交点的情况;
有两个交点的情况;
(2).运用一次函数和指数函数的图象和性质,可得值域,讨论![]() ,
,![]() 两种情况,即可得到所求
两种情况,即可得到所求![]() 的范围.
的范围.
解:(1).作出![]() 的图象,
的图象,
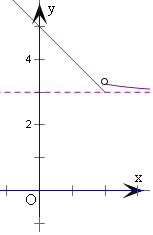
由![]() 时方程
时方程![]() 有两个不同的实根,
有两个不同的实根,
可得![]() ,且
,且![]() ,
,
即有![]() ;
;
(2)函数![]() ,
,
当![]() 时,
时,![]() 时,
时,![]() ,
,
![]() 时,
时,![]() 递减,
递减,
可得![]() ,
,
![]() 的值域为
的值域为![]() ,
,![]() ,可得
,可得![]() ,
,
解得![]() ;
;
当![]() 时,
时,![]() 时,
时,![]() ,
,
![]() 时,
时,![]() 递增,
递增,
可得![]() ,
,
则![]() 的值域为
的值域为![]() ,
,![]() 成立,
成立,![]() 恒成立 .
恒成立 .
综上可得![]() ,
,![]() ,
,![]() .
.
故答案为:(1). (3,![]() ) (2). [
) (2). [![]() ,1)∪(1,+∞).
,1)∪(1,+∞).

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目