题目内容
(本小题16分)设双曲线: 的焦点为F1,F2.离心率为2。
的焦点为F1,F2.离心率为2。
(1)求此双曲线渐近线L1,L2的方程;
(2)若A,B分别为L1,L2上的动点,且2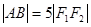 ,求线段AB中点M的轨迹方程,并说明轨迹是什么曲线。
,求线段AB中点M的轨迹方程,并说明轨迹是什么曲线。
(1)由已知双曲线的离心率为2得: 解得a2=1, ……2分
解得a2=1, ……2分
所以双曲线的方程为 , ……4分
, ……4分
所以渐近线L1,L2的方程为 和
和 =0 ……6分
=0 ……6分
(2)c2=a2+b2=4,得c=2 ,所以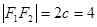 ,
,
又2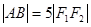 所以
所以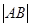 =10 ……8分
=10 ……8分
设A在L1上,B在L2上,设A(x1, ,B(x2,-
,B(x2,-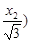
所以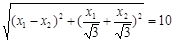 即
即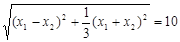 ……10分
……10分
设AB的中点M的坐标为(x,y),则x=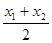 ,y=
,y=
所以x1+x2=2x , x1-x2=2 y
y
所以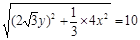 整理得:
整理得: ……14分
……14分
所以线段AB中点M的轨迹方程为: ,轨迹是椭圆。 ……16分
,轨迹是椭圆。 ……16分
【解析】
试题分析:(1)由已知双曲线的离心率为2得: 解得a2=1, ……2分
解得a2=1, ……2分
所以双曲线的方程为 , ……4分
, ……4分
所以渐近线L1,L2的方程为 和
和 =0 ……6分
=0 ……6分
(2)c2=a2+b2=4,得c=2 ,所以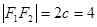 ,
,
又2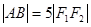 所以
所以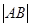 =10 ……8分
=10 ……8分
设A在L1上,B在L2上,设A(x1, ,B(x2,-
,B(x2,-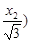
所以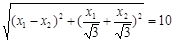 即
即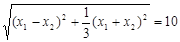 ……10分
……10分
设AB的中点M的坐标为(x,y),则x=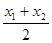 ,y=
,y=
所以x1+x2=2x , x1-x2=2 y
y
所以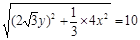 整理得:
整理得: ……14分
……14分
所以线段AB中点M的轨迹方程为: ,轨迹是椭圆。 ……16分
,轨迹是椭圆。 ……16分
考点:本题主要考查双曲线的标准方程及几何性质,轨迹方程的求法。
点评:点评:求曲线的轨迹方程是解析几何的基本问题,本题利用相关点法求轨迹方程,相关点法 根据相关点所满足的方程,通过转换而求动点的轨迹方程.中档题。

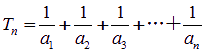 ,是否存在正整数k,使得当n≥3时,
,是否存在正整数k,使得当n≥3时,