题目内容
(本小题16分)已知点A(-1, 0)、B(1, 0),△ABC的周长为2+2.记动点C的轨迹
为曲线W.
(1)直接写出W的方程(不写过程);
(2)经过点(0, )且斜率为k的直线l与曲线W 有两个不同的交点P和Q,是否存在常数k,使得向量![]() 与向量
与向量![]() 共线?如果存在,求出k的值;如果不存在,请说明理由.
共线?如果存在,求出k的值;如果不存在,请说明理由.
(3)设W的左右焦点分别为F1、 F2,点R在直线l:x-![]() y+8=0上.当∠F1RF2取最大值时,求
y+8=0上.当∠F1RF2取最大值时,求![]() 的值.
的值.
解:(1) W: ![]()
![]() .
.
(2) 设直线l的方程为![]() ,代入椭圆方程,得
,代入椭圆方程,得![]() .
.
整理,得![]() . ①
. ①
因为直线l与椭圆有两个不同的交点P和Q等价于
![]() ,解得
,解得![]() 或
或![]() .
.
设P(x1,y1),Q(x2,y2),则![]() =(x1+x2,y1+y2),
=(x1+x2,y1+y2),
由①得![]() . ②
. ②
又![]() ③
③
所以![]() 与向量
与向量![]() 共线等价于
共线等价于![]() 将②③代入上式,解得
将②③代入上式,解得![]() .
.
所以不存在常数k,使得向量![]() 与
与![]() 共线
共线
(3)当∠F1RF2取最大值时,过R、F1、F2的圆的圆心角最大,故其半径最小,与直线l相切.
直线l与x轴于S(-8,0),![]() ∽
∽![]()
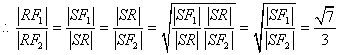 .
.

练习册系列答案
相关题目