题目内容
（本小题16分）已知平面直角坐标系
中O是坐标原点，
，圆
是
的外接圆，过点（2，6）的直线
被圆所截得的弦长为
.
（I）求圆的方程及直线的方程；
（II）设圆
的方程
，
，过圆上任意一点
作圆的两条切线
，切点为
，求
的最大值.
解：因为
，所以
为以
为斜边的直角三角形，
所以圆
：
……………………………………………………………3分
（2）1）斜率不存在时，
：
被圆截得弦长为
，所以：适合………………4分
2）斜率存在时，设：
即
因为被圆截得弦长为，所以圆心到直线距离为2所以
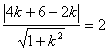
………7分
，纵上，：或
…………………8分
（3）解：设
，则
.…………10分
在
中，
，…………………………………………12分
由圆的几何性质得
，所以
，……………………………………14分
由此可得
，则
的最大值为
…………………………………………16分
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
，g(x)=x+a (a>0)(1)当a=4时，求
的最小值；（2）当
时，不等式
是定义在
上的偶函数，且
时，
． 
，
；
，求
的取值范围．
（
）．
的值域；
．
（
）．
的值域；
．
是定义在
上的偶函数，且
时，
． 
，
；
，求
的取值范围．