题目内容
若α、β为锐角,且cos(α+β)=| 12 |
| 13 |
| 3 |
| 5 |
分析:根据α、β为锐角,得到α+β和2α+β的范围,由cos(α+β)=
,cos(2α+β)=
,利用同角三角函数间的基本关系求出sin(α+β)和sin(2α+β)的值,把所求的式子中的角α变为(2α+β)-(α+β)后,利用两角差的余弦函数公式化简后,将各自的值代入即可求出值.
| 12 |
| 13 |
| 3 |
| 5 |
解答:解:由α、β为锐角,得到α+β∈(0,π),2α+β∈(0,
),
又cos(2α+β)=
>0,得到2α+β∈(0,
),
所以sin(α+β)=
=
,sin(2α+β)=
=
,
则cosα=cos[(2α+β)-(α+β)]
=cos(2α+β)cos(α+β)+sin(2α+β)sin(α+β)
=
×
+
×
=
.
故答案为:
| 3π |
| 2 |
又cos(2α+β)=
| 3 |
| 5 |
| π |
| 2 |
所以sin(α+β)=
1-(
|
| 5 |
| 13 |
1-(
|
| 4 |
| 5 |
则cosα=cos[(2α+β)-(α+β)]
=cos(2α+β)cos(α+β)+sin(2α+β)sin(α+β)
=
| 3 |
| 5 |
| 12 |
| 13 |
| 4 |
| 5 |
| 5 |
| 13 |
=
| 56 |
| 65 |
故答案为:
| 56 |
| 65 |
点评:此题考查学生灵活运用同角三角函数间的基本关系及两角和与差的余弦函数公式化简求值,是一道基础题.本题的关键是将所求式子中的角α变为(2α+β)-(α+β).

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
若α、β均为锐角,且2sinα=sin(α+β),则α与β的大小关系为( )
| A、α<β | B、α>β | C、α≤β | D、不确定 |
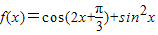 .
.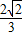 ,A为锐角,且
,A为锐角,且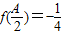 ,
,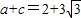 ,求△ABC的面积.
,求△ABC的面积.