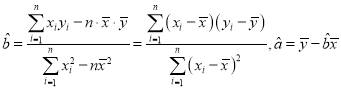题目内容
【题目】已知函数![]() .
.
(1)讨论![]() 的单调性;
的单调性;
(2)若![]() ,
,![]() 是
是![]() 的两个零点,求证:
的两个零点,求证:![]() .
.
【答案】(1)f(x)的单调递增区间为![]() ,单调递减区间为
,单调递减区间为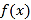 .(2)证明见解析
.(2)证明见解析
【解析】
(1)先求函数的导数![]()
![]() ,分
,分![]() 和
和![]() 两种情况讨论函数的单调性;
两种情况讨论函数的单调性;
(2)根据(1)的结果可知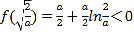 ,即
,即![]() ,利用分析法,将需要证明想不等式转化为证明
,利用分析法,将需要证明想不等式转化为证明![]() ,只需证明
,只需证明![]() ,利用函数的单调性和零点存在性定理可证明
,利用函数的单调性和零点存在性定理可证明![]() ,根据零点存在性定理和单调性证明.
,根据零点存在性定理和单调性证明.
(1)f(x)的定义域为(0,+∞),且![]() ,
,
①当a≤0时,f'(x)≤0,f(x)的单调递减区间为(0,+∞);②当a>0时,由f'(x)>0得![]() ,故f(x)的单调递增区间为
,故f(x)的单调递增区间为![]() ,
,
单调递减区间为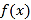 .
.
(2)∵f(x)有两个零点,∴由(1)知a>0且![]() ,∴a>2e,要证原不等式成立,只需证明
,∴a>2e,要证原不等式成立,只需证明![]() ,只需证明
,只需证明![]() ,
,
只需证明![]() .
.
一方面∵a>2e,∴![]() ,
,
∴![]() ,∴
,∴![]() ,
,
且f(x)在![]() 单调递增,故
单调递增,故![]() ;
;
另一方面,令![]() ,(x>0),
,(x>0),
则![]() ,当
,当![]() 时,g'(x)<0;当
时,g'(x)<0;当![]() 时,g'(x)>0;
时,g'(x)>0;
故![]() ,故g(x)≥0即
,故g(x)≥0即![]() 时x∈(0,+∞)恒成立,
时x∈(0,+∞)恒成立,
令![]() ,
,
则![]() ,于是
,于是![]() ,
,
而![]() ,
,
故![]() ,且f(x)在
,且f(x)在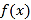 单调递减,故
单调递减,故![]() ;
;
综合上述,![]() ,即原不等式成立.
,即原不等式成立.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
【题目】某调查机构为了了解某产品年产量x(吨)对价格y(千克/吨)和利润z的影响,对近五年该产品的年产量和价格统计如下表:
x | 1 | 2 | 3 | 4 | 5 |
y | 17.0 | 16.5 | 15.5 | 13.8 | 12.2 |
(1)求y关于x的线性回归方程![]() ;
;
(2)若每吨该产品的成本为12千元,假设该产品可全部卖出,预测当年产量为多少时,年利润w取到最大值?
参考公式: